Quatre droites - solution

On donne quatre droites quelconques.
Construire une cinquième droite coupant les quatre autres en A, B, C, D tels que AB = BC = CD

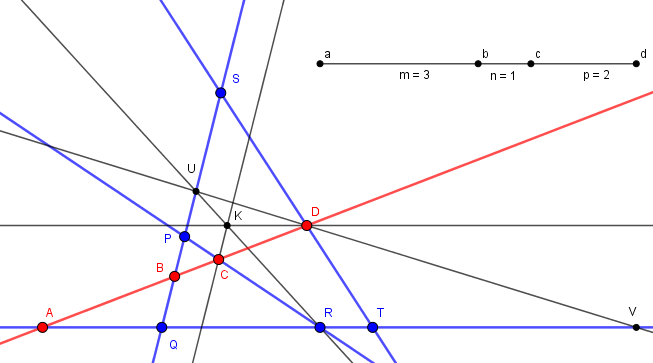
Choisissons le triangle PQR formé par trois des droites.
Traçons alors une droite (d) quelconque coupant ces trois droites pour former BC = CD.
Une telle droite s'obtient aisément en choisissant C quelconque sur PQ, puis M avec RM = 2.RC, enfin la parallèle à QR en M coupe PR en B (parallélogramme MBRD).

Traçons alors BA = CB pour obtenir 4 points équidistants ABCD, BCD sont sur trois des droites données.
Nous allons nous intéresser au lieu de A lorsque (d) varie, c'est à dire quand C varie.
Bien entendu, le lieu de C est la droite PQ, celui de B est la droite PR.

Traçons la parallèle à PQ en B et la parallèle à QR en C. Elles se coupent en E, milieu de BH.
Choisisons Q comme origine, et des axes de coordonnées affines QR, QP.
E est donc l'image de C dans une affinité de direction QP de rapport 1/2.
Le lieu de E est donc la droite RI avec I milieu de PQ.
La parallèle à PQ en A et la parallèle à QR en C se coupent en F et CF = 2.CE.
Le lieu de F est donc la droite transformée de I R par l'affinité de direction QR et de rapport 2.
C'est à dire la droite I V avec QV = 2.QR, ou encore RV = QR.
AF = 2.BE = 2.EH = 2.FK, soit KA = 3.KF. Le lieu de A est donc la transformée de la droite IV par l'affinité de direction PQ et de rapport 3. C'est à dire la droite UV avec QU = 3 QI ou encore PU = PQ/2.

On en tire la construction cherchée :

Choisir PQR, tracer U et V avec PU = PQ/2 et RV = QR.
A est sur la droite UV (le lieu précédent) et sur la quatrième droite, donc à leur intersection.
AC = 2.AB, donc C est sur une droite homothétique de PR dans l'homothétie de centre A de rapport 2, soit une droite parallèle à PR à distance double de A. Cette droite coupe PQ en C, ce qui donne la droite cherchée AC.

Discussion

Il y a à priori 4 choix possibles de PQR (4 façons de choisir la droite qui ne forme pas le triangle)
Puis trois choix possibles pour le sommet "origine" Q et 2 choix pour le rôle respectif de P et R. Soit à priori 24 solutions.
En fait ceci revient à choisir l'ordre des points ABCD sur la droite cherchée. Il y a 4! = 24 possibilités. Mais construire ABCD à partir de A donne la même solution que si on construit DCBA à partir de D, il n'y a donc que 12 solutions.
Enfin il peut y avoir moins de solutions si la droite UV est parallèle à la quatrième droite :
pas de solution pour cette droite UV là.
Si la quatrième droite est confondue avec UV, tous les points de UV conviennent comme point A :
une infinité de solutions pour cette droite UV.

Généralisation

La même construction fonctionne si AB:BC:CD = m:n:p donnés quelconques.
Le point U est alors tel que QU/QP = (m+n+p)/(m+n) et V avec QV/QR = (n+p)/n
Avec m:n:p = 1:1:1 on retrouve QU/QP = 3/2 et QV/QR = 2
Dans l'applet, les droites sont définies par les points P,Q,R,S,T déplaçables
Les valeurs de m,n,p sont définies par les points déplaçables a,b,c,d
La construction de U et V n'est pas détaillée, et seule la solution avec A sur (QR), B sur (PQ), C sur (PR) et D sur (ST) est construite

3 Droites concourantes

disons sans perte de généralité que P et S sont confondus ...
La construction précédente fonctionne encore dans ce cas, en choisissant un des triangles de sommet P.

Les 4 Droites concourantes

Dans ce cas il y a une condition nécessaire (et suffisante) sur le faisceau des 4 droites pour que ce soit possible
Dans les cas où c'est possible, alors il y a une infinité de solutions formées de droites parallèles
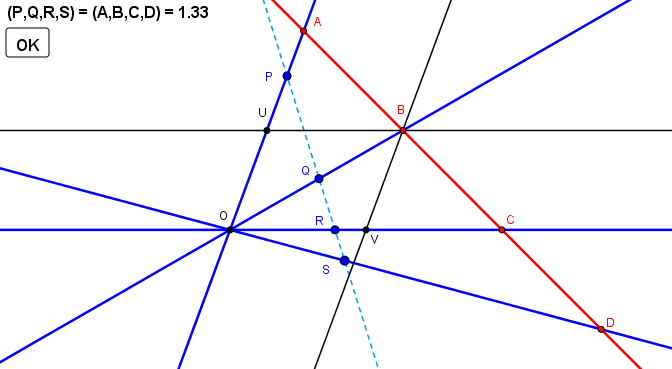
Ici les droites sont définies par les points P, Q, R, S sur une sécante quelconque
Alors si ABCD est une solution le birapport (P,Q,R,S) est égal au birapport (A,B,C,D) = 4/3

La solution n'existe donc que si le faisceau de droites a son birapport ((OP), (OQ), (OR), (OS)) = 4/3
Dans la pratique à partir d'un point B quelconque de (OQ), on construit les points A et C avec AB = BC (classique, points U et V etc)
Puis D avec CD = BC
Si ça tombe sur la droite (OS) c'est bon
et sinon cela donne la droite (OS) = (OD) qui convient.

Ainsi que par permutations (P,Q,R,S) = 4/3 ou 3/4 ou -1/3 ou -3 ou 1/4 ou 4 selon l'ordre des droites
Et dans la construction quelles trois droites sont choises au départ et de quel coté le 4ème point
Quoi qu'il en soit pour 4 droites données, une seule (direction de) solution ou aucune selon la valeur du birapport.