Fagnano - solution

Etant donné un triangle ABC, chercher le triangle DEF inscrit dans ABC avec le plus petit périmètre.

Choisissons un point D quelconque sur BC et cherchons le triangle DEF minimum pour ce point D.
Soit N le symétrique de D par rapport à AB et M le symétrique de D par rapport à AC.
Choisissons E et F quelconques sur AC et AB.
FD = FN et ED = EM.
Le périmètre DE + EF + FD = ME + EF + FN sera minimum quand la ligne brisée MEFN sera en fait une ligne droite MN : Pour ce point D choisi, le triange minimum est DE'F', de périmètre = MN.
Il s'agit maintenant de trouver le point D pour lequel MN est minimum.

L'angle MÂD = 2×CÂD et DÂN = 2×DÂB donc MÂN = 2×BÂC.
Quand D varie, cet angle reste constant et tous les triangles AMN sont semblables. AM = AD = AN, le plus petit triangle AMN sera donc quand AD minimum. Alors AD est la hauteur de ABC.

En échangeant le rôle de A,B,C, on montre de même que BE et CF sont aussi les hauteurs de ABC, et DEF est le triangle orthique, formé par les pieds des hauteurs de ABC.

Trajectoires de lumière

Rappel : les hauteurs sont les bisectrices du triangle orthique.
En d'autres termes le triangle obtenu est formé de rayons se réfléchissant sur les côtés de ABC : "trajectoire de lumière" fermée.

On peut chercher d'autres "trajectoires de lumière" se réfléchisssant plus d'une fois sur les côtés de ABC.
La réflexion sur un côté revient à poursuivre en ligne droite dans une copie par réflexion du triangle de départ.
De proche en proche on traverse ainsi des copies de ABC, et la trajectoire se referme ssi on atteint un point homologue du point de départ sur un côté homologue parallèle au côté de départ.
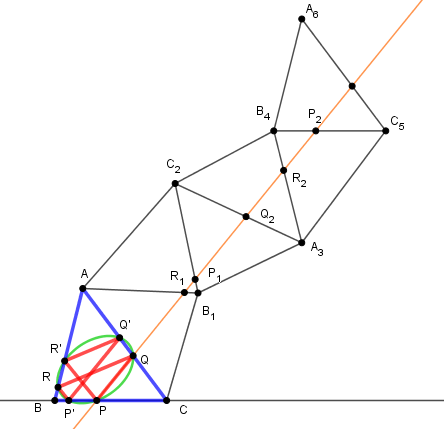
L'applet suivante construit un trajet de lumière effectuant deux tours, soit 6 copies de ABC
La direction de PQ est parallèle à la translation transformant le triangle de départ en le 6ème triangle, soit parallèle à AA6.
La trajectoire existe si la droite coupe les côtés même des triangles intermédiaires.
Dans l'applet, P est déplaçable définissant diverses trajectoires de lumière (parallèles donc).
A,B,C aussi bien sûr (pour agrandir ABC par exemple...)

Bien entendu les trajets possibles sont ici parallèles au triangle orthique.
Propriétés :
Les 6 points de réflexion sont sur une même conique.
(via les homographies induites sur les côtés)

Lorsque les rayons diagonaux se coupent en un même point, c'est l'orthocentre de ABC.
Dans l'applet, cliquer sur le bouton "H" pour placer P ainsi.

Le périmètre de cette trajectoire est constant : égal à PP2, deux fois celui du triangle orthique.

Enfin il est clair que par réflexions répétées sur les mêmes côtés dans le même ordre, la duplication des triangles par réflexion donne une translation tous les 2 tours, par conséquent, si on poursuit le trajet on n'en obtient pas d'autres.

Il n'y a que deux classes de trajectoires régulières : Le triangle orthique, cycle de 1 tour (3 réflexions) Les hexagones croisés parallèles au triangle orthique, cycles de 2 tours (6 réflexions)

Pour avoir plus de variété, et un nombre de réflexions différent, il faut des trajectoires irrégulières.
Comme la trajectoire est cyclique, le dernier transformé par reflexions successives de ABC est une translation du triangle d'origine.
Le produit de deux réflexions successives, d'angle commun α est une rotation de 2α Comme on veut au final une rotation de 0 mod 2π, il faut une somme algébrique d'angles = 0 mod π. Ca tombe bien car la somme des angles de ABC vaut comme par hasard π...
Mais d'autres sommes sont possibles.
La trajectoire précédente donne les réflexions successives sur les côtés (b+c) + (a+b) + (c+a) soit une rotation totale de 2A + 2C + 2B = 0 mod 2π
La somme des rotations = 2π donne une relation entre les angles de ABC, et donc la trajectoire n'existe que pour certains triangles, à moins que cette relation soit une identité 2n(A + B + C) = 0.

Par exemple les 4 reflexions sur (b+a) + (c+a) = -2C + 2B ne sont possibles que si le triangle est isocèle (B = C)

Les réflexions en Q et R sont perpendiculaires aux côtés.
Si A est aigu, P est libre sur tout le côté BC, si A est obtus, seule une partie de BC convient.

Les réflexions (b+a) + (c+a) + (c+a) = -2C + 2B + 2B ne sont possibles que si C = 2B.
Dans l'applet suivante ABC est contraint par C = 2B, l'angle B étant défini par le point déplaçable vert

Noter que le trajet fait un aller-retour sur lui-même et que les réflexions en Q et P' sont à 90°

Une autre suite de réflexions : (b+c) + (a+c) + (b+a) = 2A - 2B - 2C = 0 mod 2π impose A = 90°,

Les réflexions sur l'hypothénuse sont perpendiculaires à celle-ci et là aussi le trajet fait un aller-retour sur lui-même.
Le segment QR est antiparallèle à BC.

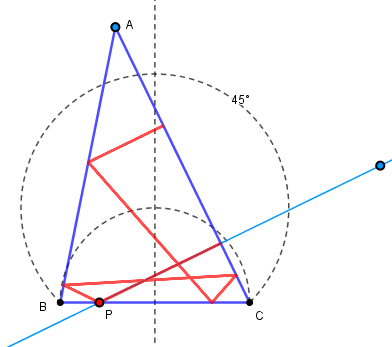
Une réflexion valable pour tous les triangles avec angle A < 45° :
La succession des réflexions est (b+c)+(b+c)+(a+b)+(c+b)+(c+a) = 2A + 2A + 2C - 2A + 2B = 2(A+B+C) = 0 mod 2π

Lorsque P est le pied de la hauteur de A les deux boucles de la trajectoire fusionnent en une seule (bouton "Ha")
Prouvez que les points d'auto-intersection S du trajet sont sur la droite AO joignant A au centre du cercle circonscrit (bouton "prop")
Indice : AO est isogonale de la hauteur issue de A.
Bien entendu A,B,C,P sont draggables, et il est recommandé de grossir ABC pour mieux observer la trajectoire (mais alors on perd les triangles réfléchis successifs...)

Une applet générique affichant le trajet pour une direction initiale quelconque du rayon issu de P.

A,B,C,P et la direction du rayon issu de P (point cyan) sont déplaçables.
Les boutons placent A et/ou l'angle du rayon sur les valeurs indiquées :
- perpendiculaire à AC ou à AB
- angle A (triangle orthique et P idoine)
- angle 2A (pentagramme si A < 45° et P adéquat)
- etc
Le curseur choisit le nombre de réflexions affichées.
En dehors de coup de bol faramineux et des positions précablées, le trajet ne se referme pas.
Sauf condition très précise sur les angles de A,B,C, et du rayon, la trajectoire passe infiniment près de chaque point de la surface de ABC. Et une variation infime d'un de ces paramètres, ou de la position de P provoque un changement complet du trajet. Le système est qualifié d'ergodique.
La valeur initiale de l'applet affiche un trajet effectuant un aller-retour sur lui-même. (d ⊥ AC)
Les réflexions successives sont (b+a)+(c+b)+(a+c)+(b+c)+(a+b)+(c+a) = -2C - 2A - 2B + 2A + 2C + 2B = 0,
garantissant que ce trajet fonctionne pour tout triangle, dans certaines limites.
Pour un triangle quelconque, il existe toujours des valeurs (très) particulières de l'angle du rayon pour lesquelles la trajectoire se referme cycliquement.
Il peut exister alors un point P particulier pour lequel le circuit se referme en moitié moins de tours (phénomène de tourniquet) :
Si la trajectoire est considérée comme une application φ de BC → BC transformant P en lui même, c'est à dire φⁿ = I l'identité, ce point est le point fixe de la transformation φ^n/2.
L'applet ne détermine pas automatiquement des points fixes et des trajectoires cycliques, vous devez essayer par vous même à la main, en dehors des cas "précablés"... bonne chance.