Locus

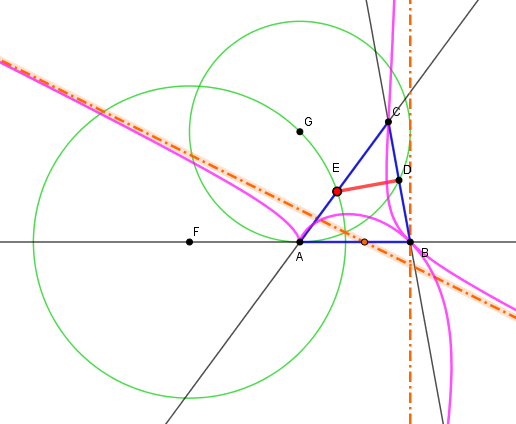
Etant donnés A et B, trouver le lieu de C pour que D sur BC et E sur AC avec AE = ED = DB et DE _|_ BC.

Les lieux de D et E sont deux cercles, d'où la construction.
Il faut aussi considérer le symétrique par rapport à la droite AB, pour les autres variantes de DE.
Déplacer E à la souris pour tracer le lieu de C.

Autre méthode

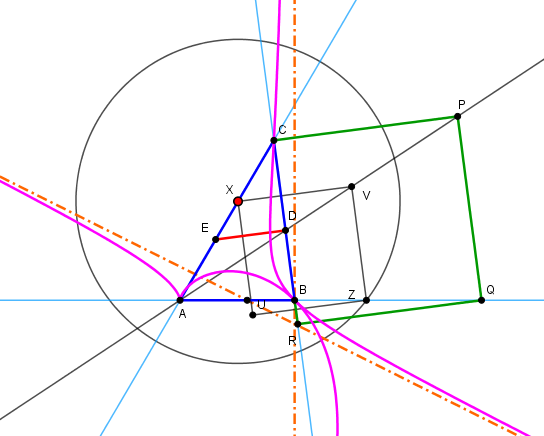
Sur le côté BC, construire un carré CPQR de côté = AC avec Q sur la droite AB.

Déplacer le point X pour faire pivoter AC et tracer le lieu de C.
DE est intérieur à ABC seulement pour arctan(1/2) ≤ θ ≤ π/2 (avec θ = BAX)
Le lieu est composé de deux parties : une pour 0 ≤ θ ≤ π correspond à B sur le segment CR (CB.CR > 0) l'autre pour pi ≤ θ ≤ 2π à C entre B et R (CB.CR < 0).
Indéfini pour θ = π/2 ou -arctan(1/2) (asymptotes)
mais où est exactement l'asymptote à -arctan(1/2) ?

Cette méthod construit un carré XVZU convenable à partir d'un point X quelconque, puis construit l'homothétique de centre A.