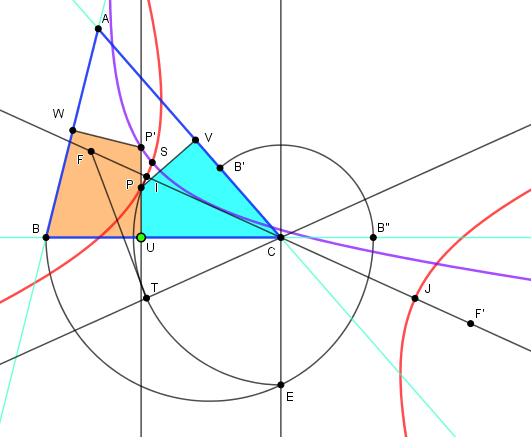
Partage du champ

Etant donné un champ triangulaire ABC, trouver un point P tel que les perpendiculaires en P aux côtés du champ découpent ce champ en trois parties d'aires égales.

Cherchons déja à construire, étant donné la projection U sur BC, un point P avec Aire(PUCV) = Aire(ABC)/3
On obtient ainsi un lieu de P.
Si on opère de même avec PUBW, l'intersection de ces deux lieux donne P.
Malheureusement cette méthode ne conduit pas à une construction géométrique exacte de P car les lieux en question sont des hyperboles.

A,B,C,U sont déplaçables.

Donnons tout d'abord une construction géométrique de P, pour U donné, avec Aire(PUCV) = Aire(ABC)/3 = S/3
Le point B' au tiers de AC donne un triangle BB'C d'aire S/3
Soit V' l'intersection de la perpendiculaire en U à BC avec AC.
Soit V" le point avec Aire(UV"C) = Aire(BB'C) = S/3. Ce point s'obtient simplement par BV" // UB'
L'aire de UV'C dépasse S/3 de l'aire de V'UV", PV est donc obtenu en construisant un triangle PVV' d'aire égale à celle de V'UV".
On a les relations :
Aire(V'V"U)/Aire(V'CU) = V'V"/V'C     (triangles V'V"U et V'CU de même sommet U)
et Aire(V'PV)/Aire(V'CU) = (V'P/V'C)²     (triangles semblables)
D'où on tire V'P = √V'C.V'V" et une construction géométrique de V'P, dont le détail est laissé au lecteur.
Lorsque l'angle en C est droit, la construction du rectangle PUCV échoue par la méthode précédente, mais il y a alors beaucoup plus simple, et le lieu de P est bien sûr dans ce cas une hyperbole équilatère CU.CV = S/3
Lorsque l'angle C est obtus, il faut tenir compte des signes des aires, et au final la relation est la même.
Si C est encore plus obtus, il n'y a même plus de solution car P avec Aire(PUCV) = S/3 est toujours extérieur à ABC, voire le polygone est croisé, et il faut alors compter son aire algébrique.

Calculons donc ces lieux de P avec Aire(PUCV) = S/3
Posons CU = u et CV = v, PU = x et PV = y.
On a alors les relations :
x² + u² = y² + v² [1] (Pythagore)
tg(C) = (tg(PCU) + tg(PCV)) / ( 1 - tg(PCU).tg(PCV)) = (x/u + y/v) / (1 - xy/uv) = (xv + yu)/(uv - xy)
soit (xv + yu) = (xy - uv)tg(C) [2]
2S/3 = xu + yv (aire du quadrilatère), soit yv = 2S/3 - xu [3]
On fait apparaître les termes en yv dans les equations [1] et [2] pour éliminer v avec [3]
et on élimine y² entre ces deux équations, ce qui après simplification donne :
(u² - x²)tg(C) + 2u.x.tg²(C) - 2S/3(1 + tg²(C)) = 0 qui est clairement l'équation d'une hyperbole équilatère.

en poursuivant un peu les calculs on obtient une caractérisation (et donc une construction) géométrique de ces hyperboles l'axe focal est la bissectrice de B et le centre B
et donc(équilatère) les asymtotes à 45° de cette bissectrice
les sommets I et J et le cercle principal, de rayon R² = CB.CB'
et donc (classique) les foyers F et F'