Menuiserie

Un menuisier veut couper un cube par un plan passant par trois points donnés.

Sur une vue en perspective du cube

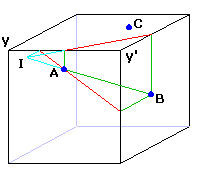
Cherchons à tracer l'intersection I de la droite AB avec le plan de la face supérieure abcd du cube.
Un plan perpendiculaire à abcd contenant cette droite est IkB. d'où la construction :
Les parallèles Ah et Bk aux arêtes verticales du cube sont tracées.
La droite hk et la droite AB se coupent en I.
Comme I fait aussi partie du plan ABC, la trace de ABC sur la face abcd est la droite CI.
On obtient alors les intersections avec les arêtes de cette face abcd, puis les droites mA → n, puis nB → p et finalement pq (ici sur la face arrière).
Si la droite IC ne coupe aucune des arêtes ab et bc (communes avec les faces des points A et B) cette construction directe des traces passant par A et B échoue. On a au moins la trace passant par C, sur abcd.

En recommençant alors la même construction pour l'intersection de BC avec la face contenant A, et de AC avec la face contenant B, on obtient les traces sur les plans de A et B.
Si l'intersection est "à l'infini", on trace des parallèles.

Profitons en pour donner une construction d'une droite passant par un point donné et par le point d'intersection de deux droites données, lorsque ce point d'intersection est en dehors des limites de l'épure, voire rejeté à l'infini sans qu'on le sache.

Traçons une sécante commune AB quelconque ne passant pas par P
Une parallèle quelconque A'B' à AB
Enfin la parallèle à AP en A' et la parallèle à BP en B' se coupent en P'
La droite PP' passe par le point d'intersection des droites données (homothétie).

Directement sur le cube

Il s'agit d'un problème classique de géométrie descriptive : trouver les traces d'un plan.
Considérons les deux plans de projection contenant A et C.
Le plan dont on cherche les traces est défini par les droites AB et BC.

On peut tout d'abord construire les projections de ces droites sur les plans de projection, ici de la droite AB.

Pour "voir" la suite, il faut maintenant sortir du cube et prolonger les images ainsi obtenues, jusqu'à obtenir la trace de AB.
On obtient ainsi I intersection de AB avec le plan de C

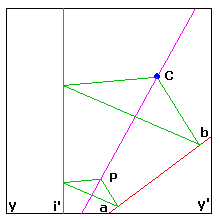
La figure en perspective ci-dessus se traduit par une épure de géométrie descriptive.
Le "plan frontal" est le plan (C), le plan "horizontal" le plan (A), la ligne de terre yy' l'arête commune.
Bien entendu le tracé de (i,i') sur cette épure est immédiat.
La trace de (ABC) sur le plan (C) est alors sur cette épure la droite (ci,c'i').

La difficulté est de reporter ceci sur les faces du cube !
En effet la droite ab est tracée sur la face (C) et ne peut être prolongée en ai sur cette face.

Sur l'épure, considérons alors le symétrique d de i par rapport à yy'.
Nous pouvons construire d sur la face (C) elle même, la droite da étant la réflexion en a de la droite ab.

Il reste à construire le trajet cd, réfléchi sur yy'.
Considérons le milieu m de cd. i' étant le milieu de di, ci est alors construite comme parallèle en c à la droite mi'.

On aurait ici aussi bien pu utiliser la technique vue précédemment : tracer sur la face (C) la droite passant par C et concourante avec la droite ab et la perpendiculaire en i', le point de concours i étant inaccessible.

L'affaire devient moins simple si (i,i') est en dehors des limites de ... l'épure !
Une solution dans ce cas est de changer de plan de coupe par un plan parallèle à (ABC).
C'est à dire d'effectuer une translation des droites AB et BC ou ce qui revient au même une translation des faces du cube.

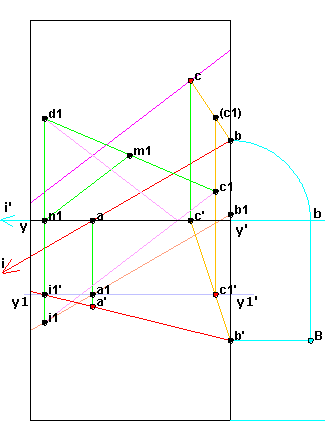
Ici on a rabaissé la face supérieure du cube.
On commence par tracer sur les faces du cube l'épure des droites AB et BC :
Le plan de projection "frontal" est ici la face (C), le plan "horizontal" la face (A) La ligne de terre est l'arête commune.
Les perpendiculaires aux arêtes en A,B,C donnent les points a,b,b',c'. a' est A lui même et c est C lui même.
On obtient ainsi les épures des droites (ab,a'b') et (bc,b'c').
Il faudrait normalement construire l'épure (i,i') du point I d'intersection de AB avec la face supérieure,
mais i' étant l'intersection de a'b' avec la ligne de terre yy' est en dehors des limites de l'épure.

Choisissons un point C1 de la droite BC, c'est à dire sur l'épure ((c1),c1').
Nous allons effectuer une coupe par un plan parallèle à (C) en C1.
Choisissons le nouveau plan frontal comme étant celui passant par C1.
Alors la nouvelle ligne de terre y1y1', passant par c1', donne la nouvelle image a1 de A et donc la nouvelle image a1b1 de ab, bien entendu comme parallèle à ab passant par a1.
Petit problème ici : ab est tracé sur la face (C) du cube, et nous avons en fait besoin de a1b1 sur la face (A). Qu'à cela ne tienne, il suffit de reporter en a1 l'angle en a avec la ligne de terre.
Dans ce nouveau repère, la droite (a'b', a1b1) coupe le plan frontal en (i1, i1') que l'on peut tracer sur la face (A).
Lors du changement de repère le point c1 a vu son image passer de (c1) à c1 : translation de vecteur aa1.
La trace du plan de coupe (ABC) sur le nouveau plan frontal est alors c1i1.
Pour la tracer on reporte n1d1 = n1i1 sur la face (C). m1 étant le milieu de d1c1 la droite m1n1 est parallèle à c1i1, donc parallèle à ci.
Ceci permettant alors de tracer ci comme parallèle à m1n1 en C. Ouf.

Finalement, en ne gardant que ce qui est effectivement tracé sur les faces du cube :

(les points A,B,C ne sont pas au même endroit que dans l'épure ci-dessus)

Si le point (c1) translaté en c1 "sort" de la face (C) lors de sa translation, on reporte le reliquat sur la face (A) et alors la droite c1i1 est directement tracée sur cette face. La droite ci sur la face (C) est construite comme faisant le même angle avec la ligne de terre.

La géométrie descriptive n'étant plus enseignée depuis longtemps, les techniques présentées ici peuvent sembler "étranges" et le vocabulaire peu connu :
ligne de terre, plan frontal, épure, trace...
Une recherche sur le net donne peu d'informations détaillées sur le sujet, surtout des généralités, ou du "dessin industriel" (vue de face, vue de dessus, vue de côté) certes directement lié à cette "géométrie descriptive", mais ce n'est pas tout à fait ça.
Il reste quelques chapitres dans d'anciens livres...