Menuiserie

Un menuisier veut couper une baguette de section triangulaire quelconque (un prisme droit) par une coupe en biais formant un triangle équilatéral.

Soient x,y,z les arêtes obtenues. a,b,c les côtés de la section droite et d le côté de la section en forme de triangle équilatéral.
Si on rallonge la baguette d'une quantité h (x+h, y+h, z+h), cela ne change rien à l'affaire et on peut donc supposer z = 0.
On a alors les relations :
d² = a² + x²
d² = b² + y²
d² = c² + (x - y)²

soit y² = a² - b² + x²
Puis a² + x² = c² + x² + y² - 2xy ou encore 4x²y² = (a² - c² - y²)² et en éliminant y entre ces deux équations :
4x²(a² - b² + x²) = (b² - c² - x²)² équation du second degré en x²,
3(x²)² + 2(2a² - b² - c²)x² - (b² - c²)² = 0
d'où x² puis y² et finalement d² constructibles à la règle et au compas.
Nous ne donnerons pas une telle construction qui bien que "pas trop" compliquée est filandreuse et artificielle.
Avec a = 3, b = 4 et c = 5 cela donne : x = 4.1144, y = 3.15095, d = 5.09198 (expressions exactes horribles)

La construction proposée maintenant fait appel à l'angle de Brocard d'un triangle et aux cercles de Neuberg.
Sans démonstration ici.

Définition : Angle de Brocard, points de Brocard
Les droites issues des sommets et faisant un angle ω avec les côtés sont concourantes en Ω, appelé point de Brocard de ABC, pour une valeur particulière de ω appelée angle de Brocard du triangle.
C'est le point de concours des cercles passant par A et tangent en B à BC, passant par B et tangent en C à CA et passant par C et tangent en A à AB.
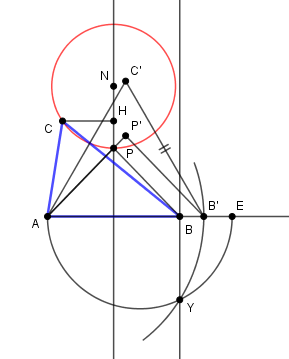
Une construction simple de l'angle de Brocard ω est obtenue par le point d'intersection P de la parallèle à AB en C et de la tangente en B au cercle circonscrit.

Le point Ω' obtenu en "tournant dans l'autre sens" définit le second point de Brocard, et le même angle ω qui est ainsi une caractéristique du triangle ABC.

Théorème : Cercles de Neuberg
Les triangles ABC ayant même base AB et même angle de Brocard ont leur point C sur un cercle appelé cercle de Neuberg (du point C).
Une propriété importante ici est que la puissance de A (et de B) par rapport à ce cercle est AB².
Une construction du cercle de Neuberg est alors :
La médiatrice de BC et la perpendiculaire en B à AB se coupent en I
La médiatrice de AB et la perpendiculaire en I à AC se coupent en N, centre du cercle de Neuberg :
Le cercle de centre I passant par C est tangent en B à AB, donc la puissance de A par rapport à ce cercle est AC.AC' = AB². Le cercle de Neuberg, centré comme il se doit sur la médiatrice de AB, et passant par C et C' donne la même puissance AC.AC'.

Théorème : Etant donné un plan (P) "horizontal" et un plan (Π) faisant un angle φ avec le précédent.
Un triangle A'B'C' équilatéral du plan (Π) se projette en ABC sur (P).
En faisant tourner le triangle A'B'C' dans (Π), tous les triangles ABC ainsi obtenus ont le même angle de Brocard, et cette rotation engendre toutes les formes de ABC avec cet angle de Brocard.
Il existe donc une relation directe entre l'angle de Brocard ω de ces triangles et l'angle φ (que nous n'expliciterons pas ici).

Et maintenant la construction annoncée.
Soit à chercher le triangle équilatéral AB"C" de (Π) qui se projette en ABC donné.
La solution est immédiate si ABC est isocèle et la base le plus grand côté : un triangle équilatéral ayant même base.
Les théorèmes précédents vont permettre de transformer ABC en un triangle isocèle de même angle de Brocard et de même aire, donc image du même triangle équilatéral, mais tourné dans (Π).

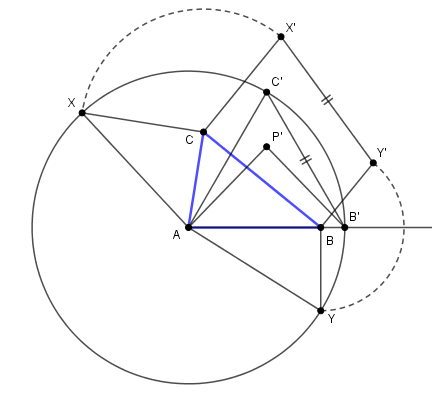
On construit donc le cercle de Neuberg de ABC, et ainsi un triangle ABP isocèle de même angle de Brocard, on choisit le plus "aplati" des deux.
Le triangle AB'P' semblable de même aire que ABC est la projection du triangle équilatéral AB'C'.
On obtient ainsi en vraie grandeur le côté d du triangle équilatéral cherché.
La construction de AB'P' est obtenue ainsi :
Construire le point E avec AE/AB = MH/MP, rapport des hauteurs, donc des aires de ABC et ABP.
Le cercle de diamètre AE coupe la perpendiculaire en B à AB en Y.
On a donc AY² = AB.AE = AB² MH/MP, puis AB' = AY
Le rapport d'homothétie de AB'P' et ABP est donc bien la racine carrée du rapport des hauteurs, donc des aires comme cherché.

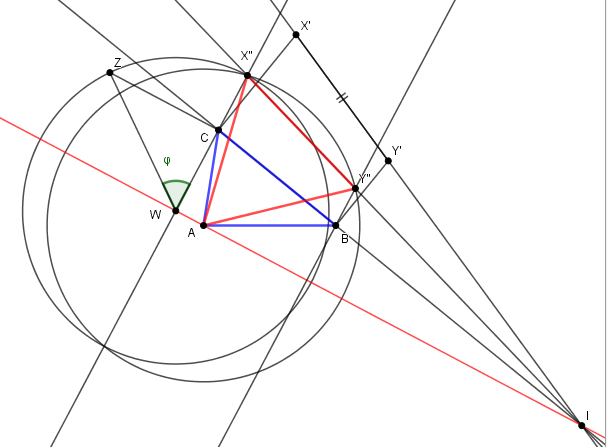
On construit alors en vraie grandeur les faces latérales :
ABB", rabattue en ABY déja tracée (AY = d, côté du triangle équilatéral)
ACC", rabattue en ACX. X sur le cercle de rayon d et sur la perpendiculaire à AC
Puis enfin la face BCC"B" rabattue en BCX'Y'
Point délicat : la construction de cette dernière face n'est correcte que si X'Y' = d !
C'est à dire si B" et C" du même côté du plan de ABC. Sinon il faut prendre le symétrique de X' ou de Y'.
... ou choisir un autre coté que AB comme point de départ (A n'est pas le point le plus bas).

Le plan de AB"C" coupe le plan de ABC selon une droite (d), passant par A puisqu'on a choisi z=0.
Considérons la face BCC"B", dont le rabattement selon la droite BC est BCX'Y').
La droite (d) passe aussi par l'intersection I de BC et B"C", donc de BC et X'Y' après rabattement.
On peut alors construire le triangle AX"Y" qui est le rabattement de AB"C" du plan (Π) sur (P) selon la droite (d).
Ceci permet de construire l'angle φ du plan de coupe (Π) :
WCZ est le rabattement du triangle WCC" le long de la perpendiculaire CWX" à (d)
On a donc ainsi construit l'orientation du plan de coupe, par (d) et φ