Triangles

Construire un triangle ABC étant données deux hauteurs h_b et h_c et la bissectrice de l'angle A = t_a

Soit T le pied de la bissectrice, TB/TC = AB/AC
D'autre part AB.h_c = AC.h_b, donc TB/TC = h_b/h_c

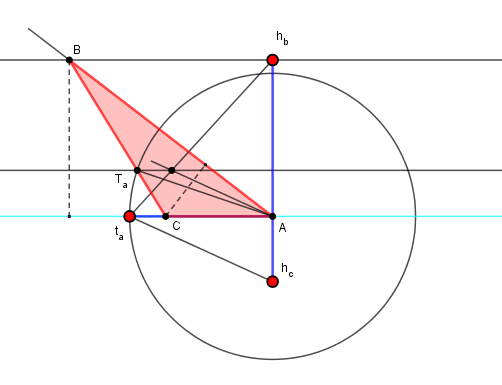Fixons A et la droite Ac.
B est sur la parallèle à Ac, à distance h_b Comme TB/TC = h_b/h_c, T est aussi sur une parallèle à Ac
Cette parallèle est construite avec Thalès à partir d'un point quelconque sur Ac (ici t_a), en projetant sur h_bt_a la division (h_b,A,h_c).
Le point T est alors construit par intersection de cette parallèle avec le cercle de rayon AT = t_a donné
L'angle TAAc est alors dupliqué pour obtenir BAT = TAAc, et le point B.
BT coupe Ac en C.

Nota : en plaçant h_b et h_c du même côté, la bissectrice AT devient la bissectrice extérieure de l'angle A.