Triangles

Construire un triangle ABC étant données hauteur h_a, médiane m_a et la bissectrice t_a de l'angle A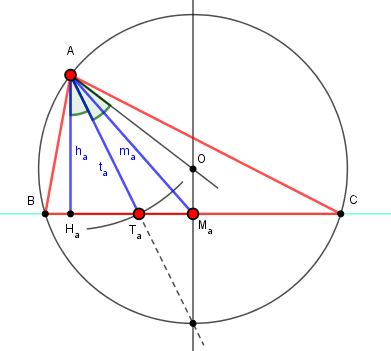

h_a m_a définissent le triangle rectangle AH_aM_a.
Lemme 1 Le pied de la bissectrice est entre le pied de la hauteur et le milieu du côté.
Lemme 2 L'orthocentre et le centre du cercle circonscrit sont isogonaux : AH et AO symétriques par rapport à la bissectrice

Sans démontrer ici ces propriétés "bien connues", nous allons les utiliser.
Il y a donc au plus un seul pied possible pour la bissectrice, si h_a < t_a < m_a : intersection du cercle de centre A de rayon t_a et de la droite H_aM_a entre H_a et M_a.
Ceci donne la direction de la bissectrice, et donc la droite AO, symétrique de AH_a par rapport à cette bisectrice.
Le centre du cercle circonscrit O est l'intersection de AO et de la médiatrice de BC, perpendiculaire à H_aM_a en M_a.
Ce cercle circonscrit (de centre O passant par A) donne alors B et C.