Cinq cercles

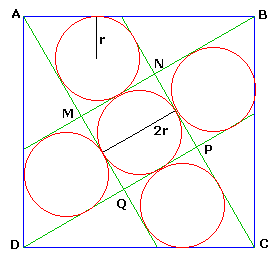
Placer cinq cercles dans un carré.

Soit a le côté du carré, r le rayon des cercles.
Soient x = AM et y = BM les côtés du triangle rectangle ABM
On a bien entendu x² + y² = a²  [1]
Mais aussi l'aire de ce triangle rectangle xy/2 = r.(x + y + a)/2  [2] (cercle inscrit)
Enfin MN = y - x = 2r  [3]
Il n'y a plus qu'à résoudre ce système de 3 équations à trois inconnues...
r s'élimine de suite et donne 2xy = (y - x)(x + y + a)
[1] donne (x + y)² - 2xy = a²
Soit (y - x)(x + y + a) = (x + y)² - a² = (x + y + a)(x + y - a)
Comme x + y + a > 0, il reste y - x = x + y - a

soit  x = a/2 

On en tire immédiatement l'angle MAB = 60°, et la construction : une fois les droites tracées, les cercles inscrits s'en déduisent immédiatement.