Grèbe
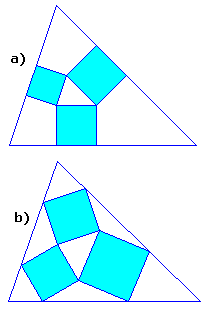
"Inscrire" trois carrés dans un triangle donné.
On considère ici deux façons d'inscrire ces trois carrés :
Dans les deux cas deux sommets des carrés servent de "liaison" entre les trois carrés,
qui se touchent ainsi par ces coins.
• a) chaque carré a ses deux autres sommets sur le même côté du triangle donné
• b) chaque carré a ses deux autres sommets sur deux côtés différents du triangle donné
a) Sur le même côté
La configuration clé est celle du Théorème de Grèbe
|
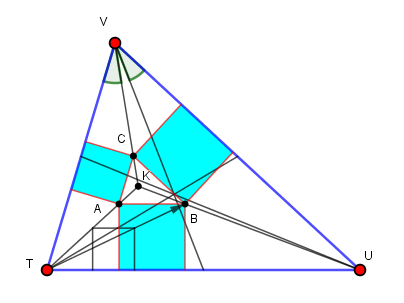
Etant donné un triangle ABC, on construit des carrés sur chaque côté
Les prolongements des 4èmes côtés de ces carrés définissent un triangle TUV AT, BU, CV sont les symédianes de ABC (et de TUV), et sont donc concourantes en le point de Lemoine K commun à ABC et TUV. K est pour cette raison parfois appelé point de Grèbe. Les deux triangles sont homothétiques de centre K. |
En ce qui concerne notre problème, le triangle donné est TUV et on cherche ABC.
On construit son point de Lemoine K.
Les carrés cherchés sont alors inscrits chacun séparément dans les triangles KTU, KUV et KTV,
d'où une construction.
Nota : si on construit le point de Lemoine de TUV par le théorème de Grèbe et des carrés extérieurs à TUV,
et ainsi un triangle T'U'V' encore plus grand, les carrés cherchés sont immédiatement construits par
l'homothétie de centre K qui transforme T'U'V' en TUV.
Cette méthode conduit à une figure "assez grande" !
Ici, tout est "à l'intérieur" de TUV, en construisant le point de Lemoine
d'après la définition des symédianes.
Le carré inscrit dans KTU est alors construit par une homothétie de centre T sur un carré quelconque dans l'angle T.
b) Sur des côtés différents
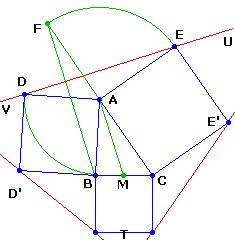
Là aussi nous allons partir à l'envers, du triangle intérieur ABC.
Considérons une rotation de 90° de centre A. Elle transforme E en F et D en B, donc DE en BF.
A est le milieu de FC. Soit M le milieu de BC. BF est donc parallèle à AM.
Les côtés de TUV sont perpendiculaires aux médianes de ABC
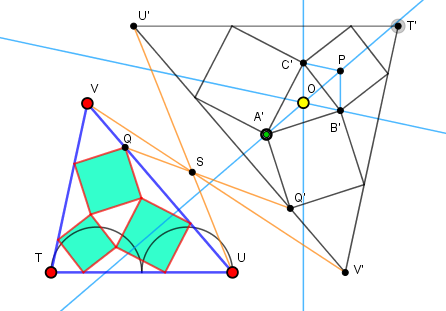Une construction de ABC à partir de TUV peut alors être :
- Construire en un point O quelconque les perpendiculaires aux côtés de TUV
- Construire un triangle A'B'C' ayant ces droites comme médianes.
- Construire à partir de A'B'C' le triangle T'U'V' correspondant
- En déduire ABC comme image de A'B'C' par la similitude T'U'V' → TUV.
La construction d'un triangle admettant trois droites données comme médianes n'offre aucune difficulté :
- Choisissons un point A' sur la médiane.
- Soit P' avec OP' = -OA' et complèter le parallélogramme OB'P'C'
(Preuve : dans un parallèlogramme, les diagonales se coupent en leur milieu)
Dans l'applet O et A' sont déplaçables.
Par construction, le triangle T'U'V' a ses côtés parallèles à TUV,
la similitude est donc une simple homothétie, dont le centre est le point
de concours S de TT', UU' et VV'.
Bien entendu on choisit le point A' pour que cette homothétie
ait un rapport suffisamment ≠ 1 (T'U' assez ≠ TU), car
sinon ce serait une translation ou presque
(S très loin).
Il n'y a bien entendu aucun problème de cette sorte si le rapport d'homothétie est négatif !
Les points de contact des carrés avec les côtés de TUV s'obtiennent ensuite par de simples intersections de droites issues de S.
La construction est toujours possible si le triangle TUV donné a tous ses angles aigus.
Sinon un des carrés peut "déborder" de TUV.
Cherchez à démontrer que l'angle obtus V doit être extérieur aux demi cercles de diamètre TU/2.
