Sangaku one more time

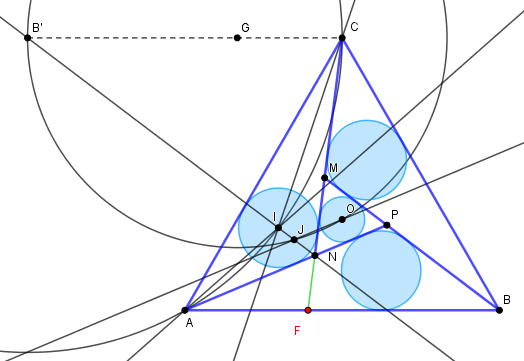
Dans un triangle équilatéral partagé "régulièrement" en quatre triangles,
les cercles inscrits dans chacun des quatre triangles sont égaux, de rayon r.

Pour une fois à vous de chercher la solution, na ! (Il y a tout ce qu'il faut dans la figure).
Dans l'applet le point F draggable permet de varier la taille des triangles, et donc des cercles inscrits.

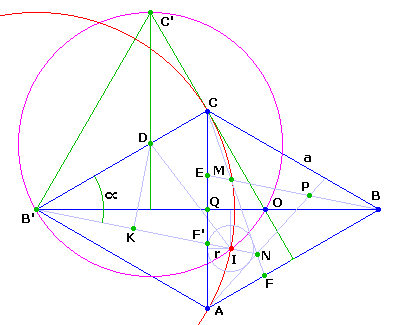
La partie "difficile" est le calcul du rayon... quoique...

CO = CQ/cos(30°)
DI = B'D = CO/cos(30°) = CQ/cos²(30°) = 2a/3
B'I = a
cos(α) = BK/B'D = 3/4, donc sin(α) =  √7/4
et finalement r = B'I.cos(α - 30°) - B'M, soit
avec cos(α - 30°) = cos(α)cos(30) + sin(α)sin(30) :

r/a = (√7 - √3)/8 ≈ 0.114212562936964...

En prime le calcul de AF/AB : AF = AF' = AQ - B'Q.tg(α - 30°)
avec tg(α - 30°) = (tg(α) - tg(30°))/(1 + tg(α)tg(30°)),
tg(α) = √7/3, tg(30°) =  √3/3, AQ = a/2 et B'Q = a√3/2 :

AF/a = (17 - 3√21)/10 ≈ 0.3252272915...