Triangle superposés

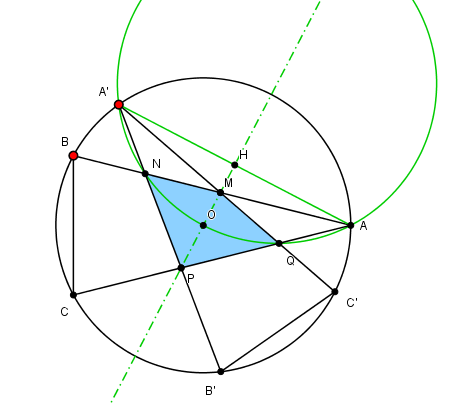
Deux triangles isocèles identiques d'angles A, (180-A)/2 et (180-A)/2
ont leurs sommets sur un même cercle.
Ils ont un déplacement angulaire entre eux de φ = 125°.
Si l'aire commune à ces deux triangles est précisément la moitié de l'aire
d'un triangle, trouver l'angle A.

A est fixe. Le point 'a' peut être déplacé pour ajuster le décalage φ
B peut être déplacé pour ajuster l'angle A.
La question est de placer B pour que le rapport des aires soit = 0.5

Calculs

La droite OM est axe de symétrie de la figure. L'angle MOA = φ/2, et aA = 2.R.sin(φ/2)
On peut alors évaluer tous les angles en A :
aAO = 90° - φ/2 du triangle rectangle OHA, donc
aAB = 90° - φ/2 - A/2 et
aAC = 90° - φ/2 + A/2

Ceci permet de calculer l'aire des triangles aPA, aQA = ANa et aMA
Et donc l'aire de MNPQ = (aPA) - 2*(aQA) + aMA
Et enfin d'exprimer que cette aire doit être le 1/2 de celle du triangle ABC.

Les détails de calculs et le deuxième cas sont laissés au lecteur.
Sans même parler de cas où l'aire commune n'est pas un quadrilatère ...

Indice :
aire d'un triangle de base c, d'angles à la base A et B
b/sinB = a/sinA = c/sin(180° - A - B) = c/sin(A+B)
Donc b = c*sinB/sin(A + B)
Et l'aire = 1/2 b*c*sinA = c²/2 * sinA*sinB/sin(A+B)

Nota : aNOQA sont cocycliques.