Coniques

Intersection de deux coniques.
Le problème consiste à construire à la règle le 4ème point d'intersection de deux coniques Γ et Γ'
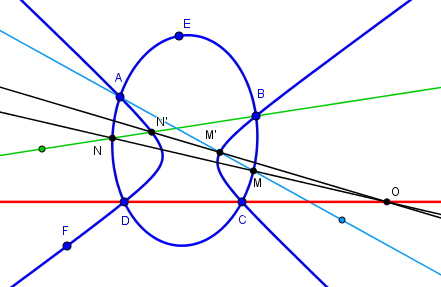
Soient deux coniques se coupant en A,B,C,D.
Une droite passant par A recoupe les deux coniques en M,M'
Une droite passant par B recoupe les deux coniques en N,N'

MN, M'N' et CD sont concourantes.

Dans l'applet ci-dessous, les coniques sont définies par 5 points, dont les 4 points ABCD et le point E pour Γ le point F pour Γ'.
Les points déplaçables cyan et verts définissent les sécantes AMM' et BNN'.

Nota : bien que par la construction de Pascal bien connue on puisse construire le "deuxième" point d'intersection de (bv) (V étant le point vert définissant la droite verte) avec Γ,
avec Géogebra pour être sûr d'avoir ce deuxième point et pas de retomber sur B lui-même, on peut de façon expéditive utiliser la commande
N = Symétrie(B, Intersection(bv, Diamètre(bv, Γ)))
Ou même faire confiance au "numérotage" des points d'intersections par Géogebra
N = Intersection(bv, Γ, 2)
Bien sur dans une vraie construction à la règle et au compas, on n'échappera pas à Pascal...

Démonstration

Appliquons le théorème de Pascal aux deux hexagones MACDBN et M'ACDBN'
Les points d'intersection I = MA.DB, J = AC.BN et O = CD.MN sont alignés, donc O est l'intersction de IJ et CD.
Sur Γ' : les points d'intersection I' = M'A.DB, J' = AC.BN' et O' = CD.M'N' sont alignés, donc O' est l'intersection de I'J' et CD.
Comme la droite MA est M'A, I = I', et de même J = J', et donc O = O'.