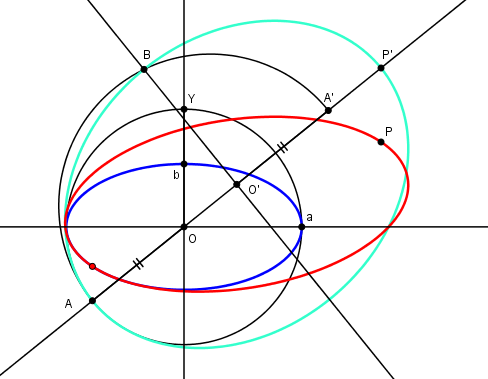
Ellipse

Ellipse minimale contenant un point et une ellipse donnés.

L'ellipse est la transformée par affinité d'un cercle.
Tout d'abord transformons l'ellipse donnée en un cercle par l'affinité inverse.
Soit P' l'image de P dans cette transformation inverse.
L'ellipse cherchée sera la transformée directe d'une ellipse de grand axe AP' = 2a' contenant le cercle et P'.
Cette ellipse contenant P' et le cercle doit avoir un rayon de courbure en A ≥ rayon du cercle.
Comme le rayon de courbure au sommet du grand axe AP' = 2a' est b²/a',
on obtient b' = O'B à partir de b² = R.a' par une construction classique.
Ceci donne l'ellipse cyan.
L'affinité directe retransforme cette ellipse en celle cherchée en rouge.