Triangle 1/7
Le 'fameux' triangle 1/7.Il est obtenu en reliant les sommets d'un triangle ABC au tiers du côté opposé.
L'aire du triangle central IJK ainsi obtenu est 1/7 de celle de ABC.
Il existe diverses façons analytiques d'obtenir ce résultat, toutefois assez laborieuses.
On s'intéresse ici aux preuves "visuelles" et à leur correction.
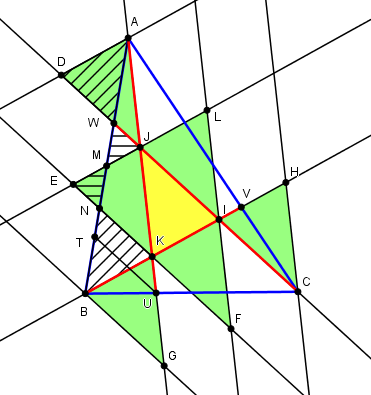
Une première "preuve" est de tracer les parallèles en IJK et ABC aux côtés de IJK.
On obtient ainsi 6 triangles verts égaux au triangle IJK.
Par symétrie, ADW est identique à BKN, et MEN identique à MJW.
Les "bouts" verts extérieurs à ABC peuvent ainsi être mis à l'intérieur,
et la surface totale des 7 triangles verts et jaune est égale à ABC,
donc Aire(IJK) = 1/7 Aire(ABC).
... mais encore faut il prouver que ces triangles sont tous égaux, ou encore que N est "l'autre 1/3" de AB, ou que M est le milieu de AB.
Et ici échoue la "preuve visuelle" car ceci est aussi compliqué à prouver que la
preuve directe et analytique que Aire(IJK) = 1/7 Aire(ABC) !
En fait cette propriété (M milieu de AB et N au 1/3 de AB) n'est vraie que parce que le
rapport de division est précisément 1/3, seule solution de 2r = 1 - r.
La valeur 1/3 doit donc apparaître explicitement dans une preuve que cette construction visuelle est correcte.
L'applet précédente montre cette propriété : en déplaçant le point U ailleurs qu'au 1/3,
on peut constater les dégâts sur la "preuve visuelle".
Le point T est le point 'catalyseur' d'une preuve élémentaire par application
successives du théorème de Thalès. L'objectif étant de démontrer que AJ = AK/2.
Une preuve quasi "directe" (sans calculs pénibles) :
U est l'homothétique de C dans l'homothétie de centre B et de rapport 1/3,
que l'on notera U = HB, 1/3(C).
De même C = HV, -1/2(A).
La composition de ces deux homothéties est une homothétie de rapport (1/3)(-1/2) = -1/6
(ce ne peut être une translation puisque ≠ 1)
Le centre de cette homothétie est aligné avec les centres B et V.
Cette homothétie transformant A en U, son centre est aussi aligné avec A,U.
Le centre de cette homothétie est donc K. C'est à dire U = HK, -1/6(A).
De même la composition des homothéties de centre C et W donne :
U = HC, 2/3(B) et B = HW, -2(A) et donc
U = HJ, -4/3(A).
Ce qui, écrit sans tenir compte des signes comme KU/1 = KA/6 = AU/7 et JU/4 = JA/3 = AU/7
montre à l'évidence que J est le milieu de AK
(AJ = 3AU/7 et AK = 6AU/7).
Les projections parallèles donnent alors que M est le milieu de AB et W le milieu de AN etc...
Autre preuve
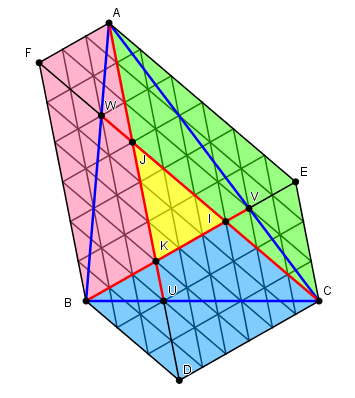
La preuve visuelle donnée sur Cut-The-Knot est "comptez les triangles"... mais ces triangles ne sont égaux que pour le rapport = 1/3 !Ceci (triangles égaux et droites visiblement concourantes) doit donc être prouvé soigneusement, comme ci-dessus (que KU = AU/7).
En fait c'est ici moins pire, car la découpe "par principe" de BC en 9 parts : 3 pour BU et 6 pour UC, égales.
Et de même pour AB et AC.
Autre preuve
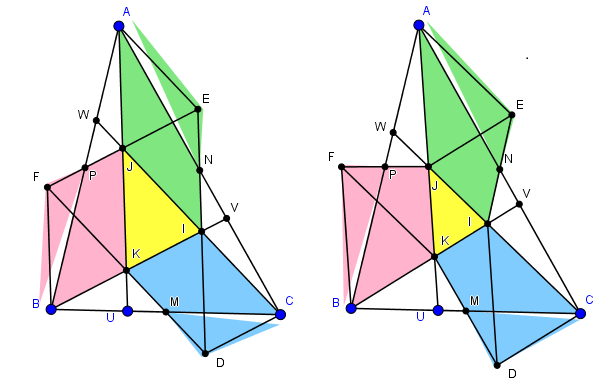
Sur le même principe, une démonstration par découpage.Les points D,E,F sont construits comme étant les symétriques de K,I,J par rapport aux milieux M,N,P des côtés.
Là encore, ceci ne fonctionne qu'après avoir prouvé sérieusement que les polygones obtenus
sont bien des parallélogrammes, et que les triangles sont égaux.
La figure est déformée et ne prouve plus rien du tout si le rapport n'est pas 1/3 (déplacer U)