Aire moitié
D'après un problème posé sur HyacinthosEtant donné un triangle ABC, O le centre de son cercle circonscrit, P un point quelconque de BC, M et N les projections de P sur AC et AB.
L'aire de AMON est la moitié de celle de ABC
Solution par Nikos Dergiades :
Rappel de quelques relations métriques :
Dans un triangle ABC, R rayon du cercle circonscrit, a,b,c les côtés et A,B,C les angles :
2R = a/sin(A) = b/sin(B) = c/sin(C) = a.b.c/2S
Aire(ABC) = S = 1/2 b.c.sin(A) = ...
Par conséquent dans un quadilatère de diagonales x, y faisant un angle θ : Aire = 1/2 x.y.sin(θ)
(en le décomposant en 4 triangles)
Ces formules étant rappelées :
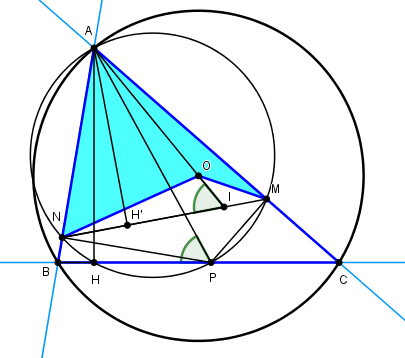Soit AH la hauteur de ABC, AH' la hauteur de AMN
AP est le diamètre du cercle circonscrit à AMPN et est conjuguée isogonale de AH' :
(AN,AP) = (MN,MP) = (AH',AM)
Comme (AN,AH) = (AO,AM) (AH et AO sont conjugués),
(AO,AH') = (AP, AH) et (AO,MN) = (AP,BC) = θ
L'aire de AMON est 1/2 AO.MN.sin(θ)
Soit avec AO = R et MN = AP.sin(A) (AP = diamètre du cercle circonscrit à AMN),
Aire(AMON) = 1/2 R.AP.sin(A).sin(θ)
L'aire de ABC est 1/2 AP.BC.sin(θ) ("quadrilatère" ABPC, de diagonales AP et BC)
Avec BC = 2R.sin(A), Aire(ABC) = R.AP.sin(A).sin(θ)
CQFD.
