Courbes de Bézier

Ces courbes sont définies par des points de contrôle P_i, 0≤i≤n
Le point courant est alors paramètré par  P(t) = ∑ P_iC_nⁱ  tⁱ(1-t)^n-i 
où les C_nⁱ sont les coefficients binomiaux (n! / i!(n-i)!) et le paramètre 0 ≤ t ≤ 1
La courbe définie par ces n+1 points est donc de degré n.
Une propriété importante est qu'elle est tangente aux deux segments extrèmes P₀P₁ (en P₀) et P_n-1P_n (en P_n).
Malheureusement, chaque point intermédiaire influe sur l'ensemble de la courbe.
Il est donc peu commode de choisir les points de contrôle pour obtenir une courbe passant par exemple par des points donnés.
On se restreint alors à une définition par morceaux, chaque morceau étant défini par 3 ou 4 points.

Construction de Casteljau

On remarque que ∑C_nⁱ  tⁱ(1-t)^n-i = (t + (1-t))ⁿ = 1
P(t) est donc le barycentre des points P_i affectés des poids correspondants.
L'associativité des barycentres permet alors de diminuer récursivement le nombre de points.

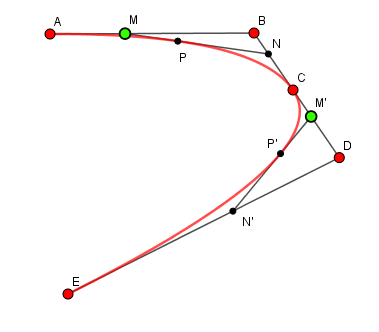Avec 3 points de contrôle A, B, C cela donne :
Soit M le barycentre de A(t), B(1-t) et N le barycentre de B(t) et C(1-t)
c'est à dire AM/AB = BN/BC = t
On calcule alors que P est le barycentre de M(t) et N(1-t) : MP/MN = t
La courbe ainsi obtenue étant de degré 2, c'est un arc de conique, et plus précisément un arc de parabole.

On peut poursuivre avec les points de contrôle suivants D, E pour une deuxième courbe de Bézier CDE "dans le prolongement" de la première.
Si on impose (comme dans l'applet ci-dessus), que BCD soient alignés, la courbe complète admet une seule tangente en C et est "lisse".
Si B et D sont du même côté de C, on crée un point de rebroussement.
Si on dissocie les directions de BC et CD, on crée un point anguleux en C.

Dans l'applet, on peut déplacer les points de contrôle A,B,C,D,E,
D étant astreint à être sur la droite BC.
Les points déplaçables M (M') définissent le paramètre t du point courant P (P') pour chaque courbe.

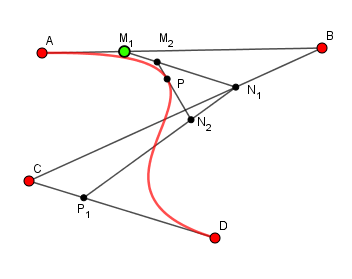La méthode ci-dessus peut être appliquée à 4 points de contrôle :
La construction de Casteljau nécessite alors une itération supplémentaire.
1ère itération : AM₁/AB = BN₁/BC = CP₁/CD = t
2ème itération : M₁M₂/M₁N₁ = N₁N₂/N₁P₁ = t
Et finalement M₂P/M₂N₂ = t

La courbe est une cubique (du 3ème degré). C'est la courbe qui est générée par l'objet CubicCurve2D de Java awt.geom, par exemple utilisée dans l'applet du jeu des "boucles".