Fractales

De façon pragmatique, elles sont définies par une de leurs propriétés les plus marquantes : l'autosimilarité. En d'autres termes, chaque morceau est semblable d'une certaine façon au tout.
Sans entrer dans une étude rigoureuse (avec introduction de ces fameuses "dimension non entière", dimensions de Hausdorff et de Minkowski), nous allons donner ici seulement quelques recettes de construction, et un petit bestiaire de quelques fractales les plus connues, ou les plus impressionnantes.

Itération et récursion

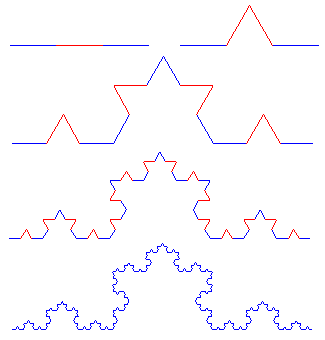
Une façon intuitive de réaliser des fractales est d'appliquer récursivement à chacun des morceaux une opération donnant d'autres morceaux. Un exemple simple est la courbe de Koch.
Partons d'un segment, que nous divisons en 3, et "plions" le segment du milieu en triangle équilatéral.
Recommençons avec chacun des 4 nouveaux segments ainsi formés, et ainsi de suite à l'infini.
On obtient ainsi une "courbe" (humm. le passage à la limite et la définition même est laissée de côté...) fractale : chacun des segments est exactement semblable au tout.

La figure montre les 4 premières étapes, au dela la taille des bosses devient inférieure au pixel !
Ceci est général, même si d'un point de vue mathématique la récursion est à poursuivre à l'infini, on ne peut obtenir qu'une visualisation approchée d'une fractale : personne n'en a jamais réellement vu une ! Dans la pratique, après quelques étapes, on a une bonne idée de l'allure de la courbe.

L-System

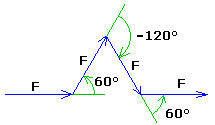Ou "système de Lindenmayer". Il s'agit de la description de règles d'une "grammaire formelle", appliquée au tracé style "tortue" : On désigne chaque segment tracé par 'F' et une rotation de ± α par '+' ou '-'

Prenons l'exemple de la courbe de Koch ci-dessus, où α = 60°. En parcourant la courbe, chaque segment 'F' est remplacé par 'F+F--F+F'
Le L-System est alors défini par son état de départ appelé son "axiome" : F et par la ou les règles de transformation : F → F+F--F+F

Koch { 
  Angle 6  ; 1/6 tour = 60°
  Axiom F
  F=F+F--F+F
}

on obtient ainsi successivement à partir du segment initial 'F'
F+F--F+F, puis en remplaçant formellement chaque 'F' par 'F+F--F+F'
F+F--F+F + F+F--F+F -- F+F--F+F + F+F--F+F etc...

Divers programmes permettent de tracer des fractales à partir de leur définition en L-system.
On obtient des structures arborescentes en plaçant des '[' et ']'. '[' mémorise la position actuelle et ']' y revient.
Les détails de syntaxe pour le programme fractint sont en annexe.

IFS

Dans le même ordre d'idée, on peut itérer une fonction f de transformation du plan.
Les règles de transformation seront ici des transformations affines, soit :

(x) → (a  b)(x) + (e)
(y)    (c  d)(y)   (f)

mais ce n'est pas obligatoire. L'important est qu'elle soit contractante c'est à dire la distance f(z)-f(z') est inférieure à celle de z-z'.

Le 'S' de IFS = Iterated Function System, est pour système de fonctions itérées On définit donc un système de telles fonctions f_i
Le résultat consiste à chercher l'ensemble S des points fixes de l'ensemble des f_i. c'est à dire S = ∪f_i(S)

Dans la pratique pour tracer cet attracteur, on prend un point au hasard, on lui applique itérativement une des fonctions f_i au hasard et on trace le point 'final'.
On peut aussi partir d'un point donné une fois pour toutes, et appliquer toutes les séquences de f_i jusqu'à une profondeur fixée. (on peut les tirer au hasard, chacune étant alors affectée d'une probabilité).

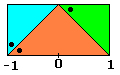Définissons ainsi par exemple le dragon de Levy.
f1 transformera le triangle rouge en triangle bleu
f2 le triangle rouge en triangle vert

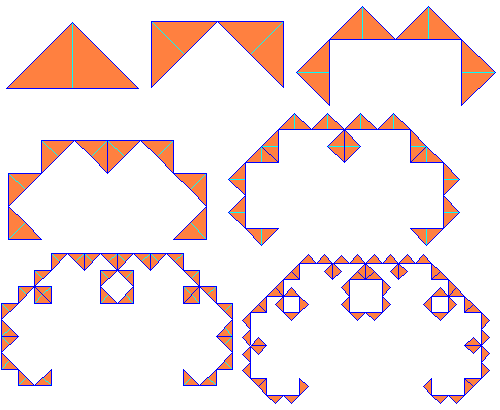
f1 : (x) = (0.5  -0.5)(x) + (-0.5)
     (y)   (0.5   0.5)(y)   ( 0.5)

f2 : (x) = (0.5   0.5)(x) + (0.5)
     (y)   (-0.5  0.5)(y)   (0.5)

Attention à l'orientation des triangles ! (indiquée par le point)
Et finallement :

Ce dragon de Levy est décrit en L-system beaucoup plus simplement

Levy {
  Angle 8 ; 45°
  Axiom F
  F=+F--F+
}

Bon, on finit par avoir un bon paquet de '++++++++...' de cette façon, alors qu'on pourrait les annuler modulo 8 (45° = 360/8), là on tourne sur place avant de tracer effectivement le segment. Et puis '-+' = ... rien du tout !
Mais il est illégal de mettre des règles de remplacement sur + et -

Dragons

La première "courbe du dragon" historique suit une règle simple que l'on va décrire en L-system

MonDragon {
  Angle 4  ; 90°
  Axiom FX
  X=X-YF-
  Y=+FX+Y
}

Les 'X' et 'Y' permettent de dupliquer le demi dragon par "pliage" et rotation, ils n'ont aucun effet sur le tracé proprement dit qui ne trace que les 'F' et tourne sur les + et -

et en IFS :

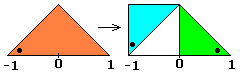
f1 : (x) = (0.5  -0.5)(x) + (-0.5)
     (y)   (0.5   0.5)(y)   ( 0.5)

f2 : (x) = (-0.5  -0.5)(x) + (0.5)
     (y)   (0.5   -0.5)(y)   (0.5)

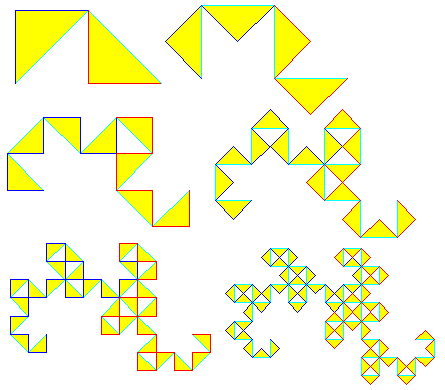On remarque juste quelques changements de signes dans la fonction f2 par rapport au dragon de Levy !
Ceci se visualise sur les règles de transformation du triangle rouge en bleu (f1) et vert (f2) Remarquer l'orientation des points !

On obtient ainsi le "dragon de Heighway".

Mais il y a bien d'autres "dragons" de ce genre...

Ensembles de Mandelbrot et de Julia

L'une des définitions les plus fructueuses concernant les fractales est par le plan complexe : chaque point (x,y) étant repéré par un nombre complexe x + iy.
On peut alors effectuer une transformation z → f(z) quelconque et itérer f. On s'intéresse alors au devenir de ces itérations, selon le point de départ.
En particulier il y a plusieurs destins possibles :

Le point "part à l'infini"
Il reste "à proximité"
C'est un point fixe

On définit ainsi des domaines du plan.

Prenons comme exemple z → z² + c, pour c donné (complexe)
L'ensemble des points z pour lesquels f(f(f(f(...(f(z) est borné est l'ensemble de Julia pour cette valeur de c.
La frontière entre les points "prisonniers" et ceux qui "s'échappent" en fait.
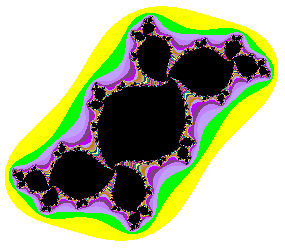
La figure montre en noir les prisonniers (ensemble de Julia rempli) pour c = -0.1 + 0.7i
Les couleurs sont les points qui s'échappent, selon leur vitesse de fuite (et à fortiori à l'extérieur de la figure).

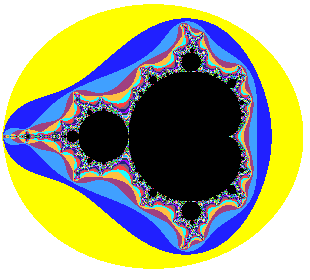Le célèbrissime ensemble de Mandelbrot part de la même fonction complexe itérée z → z² + c mais s'intéresse cette fois aux valeurs de c pour lesquelles le point 0 + 0i diverge ou est borné après itération.
Là aussi, les points noirs sont les valeurs de c pour lesquelles f⁽ⁿ⁾(0) reste bornée et les couleurs les valeurs de c qui divergent, selon leur vitesse de fuite.
Jouer avec un programme affichant des zooms sur des parties choisies de l'ensemble de Mandelbrot est une exploration peu couteuse d'un univers riche et infiniment renouvelé...

Autres fractales

On trouvera d'autres types de fractales, dont nous ne parlerons pas d'avantage ici, dans la littérature, ou en explorant les possibilités du programme Fractint par exemple.
Citons en vrac parmi les plus célèbres les attracteurs de Henon et de Lorenz, le triangle de Sierpinsky, les phénomènes chaotiques de biffurcation, d'aggrégation par diffusion, le fonctionnement d'automates cellulaires etc...

Plantes et montagnes

La nature est remplie de formes quasi fractales.
On a ainsi cité les côtes (bretonnes, norvégienne etc. selon les auteurs)
Bien entendu, ceci n'est qu'une approximation, on ne peut descendre à l'échelle des atomes ! et même là il faudrait poursuivre...
Il faut remarquer que la "similarité" dont on parle n'est pas forcément celle des triangles semblables ! mais peut se manifester dans d'autres paramètres, comme la distribution statistique des valeurs.

L'autosimilarité se manifeste de façon flagrante chez certaines plantes, citons l'archi connu chou "romanesco".
Certaines fougères montrent aussi une autosimilarité à un niveau appréciable.

D'où l'idée de simuler la croissance des plantes par les procédés construisant des fractales. Bien sûr en s'arrêtant à un niveau de récursion raisonnable.
Ceci conduit à des programmes dessinant des plantes imaginaires tout à fait réalistes.

Cette "fougère" et cet "arbre" sont tracés par quelques lignes en IFS et en L-system.
On peut de même avec ces procédés fondés sur l'autosimilarité dessiner des montagnes, des nuages etc... artificiels d'un réalisme saisissant.
Comme les objets naturels ont une nette propension à être autosimilaires, on a même étudié des algorithmes de compression d'images naturelles efficace utilisant ce procédé.
Enfin on peut composer de la "musique" (!) à partir de ces règles d'autosimilarité.
Nous en resterons là.