Parabole par 3 points

Parabole définie par son sommet O, et 2 points P₁ et P₂ (O, P1 et P2 non alignés).

P₁ = ( , )
P₂ = ( , )
→ Calculs

Méthode

Faux. il n'y a en vrai au maximum qu'une seule des trois paraboles qui est vraiment une parabole
Considérons une parabole d'axe Ox horizontal, de sommet O. Son équation est Y² = 2pX.
Soit m = tanθ la pente de l'axe de la parabole cherchée.
C'est à dire faisons tourner la parabole Y² = 2pX de l'angle θ. Alors les coordonnées (X,Y) après rotation de θ deviennent :
x = X.cosθ - Y.sinθ
y = X.sinθ + Y.cosθ
Ou en utilisant la rotation inverse :
X = x.cosθ + y.sinθ
Y = -x.sinθ + y.cosθ
La substitution de ces valeurs dans l'équation de la parabole horizontale donne l'équation de la parabole cherchée :
(-x.sinθ + y.cosθ)² = 2p(x.cosθ + y.sinθ)

Certes θ et p sont inconnus. Mais cette parabole passant par P₁ et P₂, ceci donne deux équations permettant de calculer ces valeurs.
En P1 : (-x₁.sinθ + y₁.cosθ)² = 2p(x₁.cosθ + y₁.sinθ)
En P2 : (-x₂.sinθ + y₂.cosθ)² = 2p(x₂.cosθ + y₂.sinθ)
En éliminant p entre ces équations, on obtient :

(-x1.sinθ + y1.cosθ)²		x1.cosθ + y1.sinθ
	=
(-x2.sinθ + y2.cosθ)²		x2.cosθ + y2.sinθ

C'est à dire, en divisant par cosθ, et en notant m = tanθ :

(-x1.m + y1)²		x1 + y1.m
	=
(-x2.m + y2)²		x2 + y2.m

Ou simplement (-x₁.m + y₁)²(x₂ + y₂.m) = (-x₂.m + y₂)²(x₁ + y₁.m)
C'est à dire une équation du 3^ème degré en m :   a.m³ + b.m² + c.m + d = 0, avec

a = x₁²y₂ - x₂²y₁
b = x₁²x₂ - 2.x₁.y₁.y₂ - x₂²x₁ + 2.x₂.y₁.y₂
c = y₁²y₂ - 2.x₁.x₂.y₁ - y₂²y₁ + 2.x₁.x₂.y₂
d = y₁²x₂ - y₂²x₁

Si a = 0, elle devient juste une équation du 2^nd degré b.m² + c.m + d = 0 et la 3^ème solution est m = ∞, c'est à dire θ = 90°.
Si d = 0, m = 0 est une solution, les deux autres sont solutions de l'équation du 2^nd degré a.m² + b.m + c = 0.
Sinon, l'équation du 3^ème degré est résolue numériquement par la méthode de Newton.

Le tracé de la parabole à partir de là est fait directement grace au théorème de Pascal.
Les 5 points utilisés sont P₁, P₂, O, O' = O, Z = point à l'infini sur l'axe.
Soit I l'intersection de P₁Z avec OP₂ (P₁Z est la parallèle à l'axe en P₁)
Choisissons un point K quelconque de OO', c'est à dire sur la tangente en O à la parabole, perpendiculaire à l'axe en O.
Soit J l'intersection de O'P₁ avec IK.
Le point courant de la parabole est alors M, intersection de KZ avec P₂J, KZ étant la parallèle à l'axe en K.
On peut aussi construire le foyer (donnant p = 2.OF) et la directrice, connaissant désormais les points et l'axe, comme fait ici

Une applet Geogebra construit la parabole connaissant l'axe (calculé comme ci dessus), le sommet et un point P1 :
tracé de la tangente au sommet, de la tangente en P1 et donc du rayon foval en P1 (P2 est redondant) :

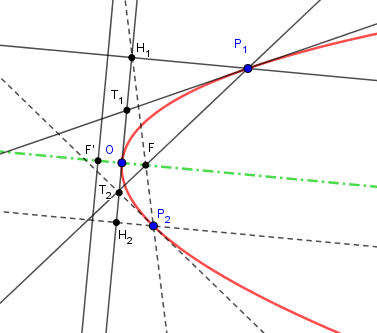
A voir si Geogebra choisit la bonne solution quand il y en a trois...