Quadrilatère inscrit

Construction d'un quadrilatère inscrit de côtés a,b,c,d donnés
(d'après de.sci.mathematik, Mehr "Vierecke fuer Dummies" id=1146916721.369663@news.aic.at, auf Deutsch)

Bien sûr si le plus grand côté est supérieur à la somme des 3 autres, le problème est impossible, il n'y a pas de quadrilatère du tout, inscrit ou pas.
Soient b et d deux côtés opposés, b ≤ d

Si b = d le quadrilatère est alors un trapèze, les côtés a et c sont parallèles, et la construction est très simple :
construire un triangle (isocèle) de côtés |a - c|, b, d = b et le "prolonger" par un parallélogramme pour obtenir un trapèze isocèle.
Si a = c, c'est en fait un rectangle.

Reste donc le cas b < d, alors les côtés a et c se coupent en E.
Les triangles EAD et ECB sont semblables (angle C = angle A) et en appelant x = BE et y = CE

x/b = (y + c)/d
y/b = (x + a)/d

soit en résolvant :
x = b(ab + cd)/(d² - b²)
y = b(bc + ad)/(d² - b²)

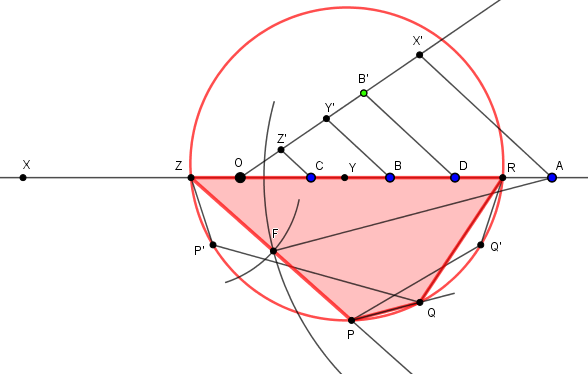
Sur une droite u'Ou on porte les distances OA = a, OB = b, OC = c, OD = d puis sur une droite Ov on reporte la distance OB' = OB
Les parallèles à DB' issues de A,B et C coupent Ov en X',Y',Z'
On reporte OX = OX', OY = OY' et OZ = OZ' sur la droite u'Ou, Y du même côté que ABCD, X et Z du côté opposé.
Alors CX = c + (b/d)×a, AZ = a + (b/d)×c et DY = d - (b/d)×b

On construit sur AZ le triangle AZF avec AF = CX et ZF = DY
Le triangle AZF est semblable aux triangles EAD et ECB de l'analyse.
Sur la droite ZF, on reporte ZP = d et on trace la parallèle à AF issue de P
Sur cette parallèle on construit PQ = c et sur la droite AZ, ZR = a
Le quadrilatère cherché est ZPQR.
Les deux autres solutions s'obtiennent en construisant P', symétrique de P par rapport à la médiatrice de ZQ, donnant ZP'QR (ou simplement ZP'=c et QP'=d)
et Q', symétrique de Q par rapport à la médiatrice de PR, donnant ZPQ'R. (ou simplement PQ'=b et RQ'=c).

L'ordre des côtés est à choisir pour que b soit suffisament différent de d mais pas trop...

Encore une...

Et finalement une dernière construction :
Construisons le triangle CMB semblable à ACD sur le côté CB.
Les angles B et D du quadrilatère ayant pour somme 180°, A,B,M sont alignés.
BM/BC = c/d permet alors de construire aisément le point M.
Comme CM/CA = b/d, C est à l'intersection du cercle de centre B et de rayon b et du cercle lieu des points CM/CA = b/d.
Cette construction à l'avantage de construire le quadrilatère à partir du côté AB fixé.
L'inconvénient est que le cercle lieu de CM/CA = b/d peut avoir un rayon très grand.
Si b=d, ce cercle devient la médiatrice de AM. L'applet échoue dans ce cas.

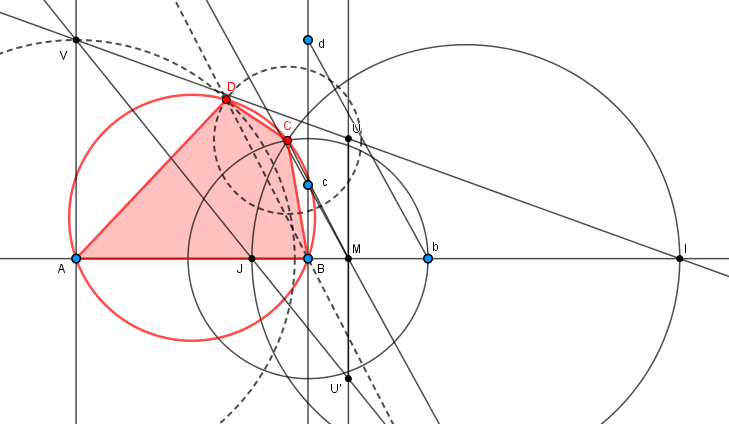
Détails :
Etant donnés AB = a, et dans le prolongement Bb = b.
Sur une droite quelconque par B (perpendiculaire par exemple), Bc = c et Bd = d.
La parallèle à bd en c coupe AB en M : BM/b = c/d.
Soient les points U et U' sur une droite quelconque passant par M, avec MU = MU' = b
Soit V le point sur une parallèle en A à UU' avec AV = d
Les droites VU et VU' coupent AB en I et J et on a IM/IA = JM/JA = b/d, le lieu de CM/CA est le cercle de diamètre IJ.
Ceci donne C, intersection de ce cercle avec le cercle de centre B, rayon b.
Puis D est obtenu comme intersection des cercles de centre A, rayon d et de centre C, rayon c.
(Ou dans l'applet, pour éviter une ambiguïté, la seconde intersection de la parallèle à CM en B avec le cercle (ABC) vu que parv définiti les triangles CMB et ACD sont semblables)