Arbelos

Etant donné un demi cercle de diamètre AB et un point C quelconque sur ce diamètre.
Tracer les demi cercles de diamètres AC et BC.
L'arbelos est la surface restante (en bleu).
La perpendiculaire en C à AB coupe le cercle en D. On montre aisément que l'aire de l'arbelos est égale à celle d'un cercle de diamètre CD    Indice

Montrer que les deux cercles inscrits dans les parties ACD et BCD de l'arbelos sont égaux. (cercles jumeaux d'Archimède)
En déduire une construction simple de ces cercles.
Détails

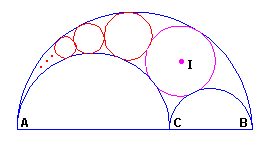Cercle inscrit - Chaine de Pappus

Un cercle intéressant dans l'arbelos est le cercle inscrit, tangent aux trois cercles de l'arbelos.
Une propriété de ce cercle :
Lorsque la forme de l'arbelos varie (le point C varie sur AB), le centre I du cercle inscrit parcourt une ellipse.
On peut poursuivre l'inscription de cercles successifs dans l'arbelos et définir une suite de cercles inscrits : la chaîne de Pappus.
Tous les centres de ces cercles sont sur une ellipse, pour un arbelos donné.
Enfin, si on choisi un rang fixé k, le lieu du centre du kème cercle de la chaîne de Pappus est une ellipse quand C varie.
Le cas k=1 (le 1er cercle inscrit) est ainsi un cas particulier d'une propriété générale pour tous les cercles de la chaine de Pappus.
Détails

D'autres propriétés du cercle inscrit Détails