Arbelos - Chaîne de Pappus

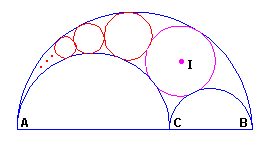Le cercle inscrit dans l'arbelos peut être prolongé en une suite de cercles tous tangents à deux des cercles de l'arbelos et au précédent de la chaîne. Il y a trois chaînes de Pappus :
Celle où les cercles sont tangents à (AB) et (AC)
Celle où les cercles sont tangents à (AB) et (BC)
Celle où les cercles sont tangents à (AC) et (BC)
Cette dernière n'est traditionnellement pas appelée "chaîne de Pappus" mais elle partage pourtant des propriétés avec les deux autres, en échangeant le rôle des trois cercles de l'arbelos, qui jouent en fait des rôles totalement symétriques dans le "plan conforme" (où les transformations de base sont les inversions).

Le premier cercle commun aux trois chaînes est bien entendu le cercle inscrit.
Nous nous bornons ici à l'étude des chaînes de Pappus proprement dites (tangentes au grand cercle de l'arbelos).
Le lecteur est invité à transposer les résultats à la troisième chaîne, en remplaçant ce qui doit l'être (par exemple ellipse en hyperbole).

Ellipse

Une première propriété assez évidente est que les centres des cercles de la chaîne sont sur une ellipse.
En effet :

Le lieu des centres des cercles tangents à deux cercles donnés est une conique

Si I est un tel centre, les points de contact avec les cercles donnés étant M et N,
O, I, M alignés et OI = R - r
O', I, N alignés et O'I = R' + r
Soit OI + O'I = R + R' = cte
De façon générale selon le "genre" de contact entre (K) et les deux cercles donnés, OI = R ± r et O'I = R ± r, et donc OI ± O'I = cte c'est à dire une ellipse (+) ou une branche d'hyperbole (-)
L'application est ici immédiate, tous les cercles de la chaine étant tangents à (AB) et (AC) [resp. (AB) et (BC) pour l'autre chaîne], leur centres sont sur une ellipse de foyer O et O'.
Nota : (BC) étant un des cercles tangents à (AB) et (AC), son centre O" est sur l'ellipse, qui a ainsi pour grand axe AO".
Dans l'applet, C et M sont déplaçables. Ici le cercle est juste tangent aux deux cercles (AB) et (AC) et peut ne pas faire partie de la chaine de Pappus.

Construction de la chaîne de Pappus

Le plus simple est de considérer l'inversion de pôle A qui conserve (BC) globalement inchangé (qui échange B et C).
Alors (AB) est transformé en la perpendiculaire en C à AB et (AC) en la perpendiculaire en B.
Le cercle inscrit et tous les cercles de la chaîne sont transformés en des cercles égaux à (BC), tangents à ces deux perpendiculaires et au cercle précédent de cette suite de cercles.
Les centres i_n et les points de contact m_n sont construits de façon évidente, en reportant le diamètre de (BC).
Le point de contact M_n de (K_n) avec (AB) est alors l'intersection de Am_n avec (AB) et I_n est l'intersection de Ai_n avec OM_n

Autres ellipses

Intéressons nous maintenant plus particulièrement au centre du cercle inscrit.
Considérons ici l'inversion de centre C qui échange A et B, et donc conserve globalement inchangé le cercle (AB).
Elle transforme le cercle (AC) en la perpendiculaire en B à AB, le cercle (BC) en la perpendiculaire en A et le cercle inscrit (K) en (k), tangent à ces deux droites et au cercle inchangé (AB).
Ce qui est important ici est que ce cercle est fixe quel que soit le point C.
Considérons le cercle Γ passant par A et B et tangent à (k) en e.
Ce cercle est globalement inchangé par l'inversion de pôle C (car passant par A et B), et donc :

Le cercle inscrit est tangent à un cercle fixe Γ quand C parcourt AB

(K) est ainsi tangent à deux cercles fixes (AB) et Γ, et donc :

Le centre du cercle inscrit parcourt un arc d'ellipse quand C parcourt AB

Précisons cette ellipse, de foyers O et F, F étant le centre de Γ
Soit x le rayon de Γ : x = Fe = FB.
Oe = 3R, en appelant R = AB/2 le rayon de (AB).
Dans le triangle rectangle FOB, OF = Oe - Fe = 3R - x et OB = R, soit (3R - x)² + R² = x², et donc  x = 5R/3 
On en déduit la position de F  OF = 4R/3 
Noter que cette ellipse à son grand axe perpendiculaire à AB, rien à voir avec l'ellipse lieu des centres des cercles de la chaîne de Pappus.
Celle-là est pour un arbelos donné (un point C donné) alors que celle qui nous intéresse ici est lorsque la forme de l'arbelos varie (C parcourt AB).

Généralisation

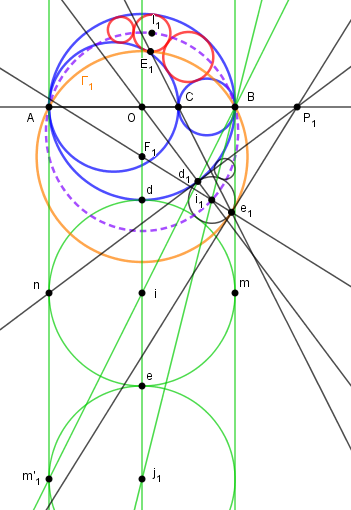On peut de même considérer le cercle passant par A et B et tangent à l'image (k_n) par inversion d'un cercle (K_n) de rang donné de la chaîne de Pappus.
Ce cercle Γ_n est alors fixe (de même que l'image de la chaîne) quand C parcourt AB, et Γ_n est globalement inchangé par l'inversion (car il passe par A et B). Par conséquent :

Quand C parcourt AB :   Un cercle de rang n donné de la chaîne de Pappus reste tangent à un cercle fixe Γn   Le centre du cercle (Kn) parcourt un arc d'ellipse,   le grand axe de cette ellipse étant sur la médiatrice de AB.

Cette ellipse passe par le centre du cercle inverse i_n... puisque ce cercle est tangent à (AB) et Γ_n !

Construction directe des cercles (k_n)
Ces cercles se construisent en considérant ensuite l'inversion de pôle B gardant (k) inchangé.
(AB) est alors transformé en la perpendiculaire en A à AB et les cercles (k_n) en des cercles tous égaux à (k), de centres j_n et tangents aux perpendiculaires à AB en A et B.
La suite de la construction est comme pour la construction des cercles (K_n) :
Les points de contact d_n avec (AB) sont l'intersection de Bm'_n avec (AB)
Le centre i_n est l'intersection de Od_n et Bj_n.

Construction du cercle Γ_n et du deuxième foyer F_n de l'ellipse (le premier foyer étant bien entendu O)
La tangente commune à (AB) et (k_n) en leur point de contact d_n (perpendiculaire en d_n à Od_n) coupe AB en P_n.
La seconde tangente de P_n au cercle (k_n) a pour point de contact avec (k_n) le point de contact e_n de Γ_n avec (k_n).
Le rayon de (k_n) perpendiculaire à cette tangente (en e_n) coupe la médiatrice de AB en F_n, centre de Γ_n et deuxième foyer de l'ellipse lieu de I_n.