Apollonius PPC

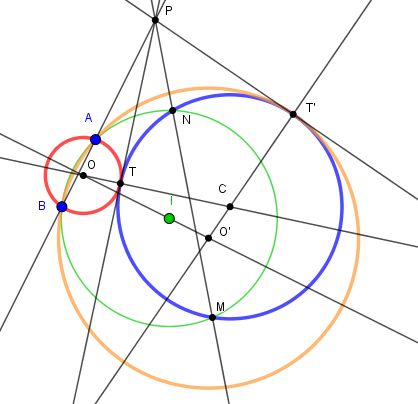
Construction des cercles tangents à un cercle donné et passant par deux points donnés.
Les points bleus sont déplaçables.
Le choix de I (déplaçable, vert) est à faire pour que le cercle de centre I coupe le cercle donné.

Un point I est choisi sur la médiatrice de AB tel que le cercle de centre I passant par A et B coupe le cercle donné en deux points M et N.
Le cercle circonscrit à ABC fait l'affaire sauf si A,B,C sont alignés.
La droite MN coupe la droite AB en P. Les tangentes PT et PT' au cercle donné fournissent les points de contact.
Les droites CT et CT' coupent la médiatrice de AB aux centres des cercles cherchés.
Bien entendu A et B doivent être tous deux extérieurs ou tous deux intérieurs à (C).

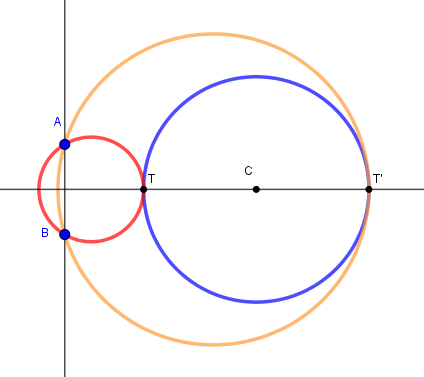
C sur la médiatrice

La construction précédente échoue si C est sur la médiatrice de AB (MN parallèle à AB).
Mais dans ce cas la construction est beaucoup plus simple :
Les points de contact T et T' sont l'intersection du cercle donné et de cette médiatrice.
Les cercles tangents sont alors les cercles circonscrits à ABT et ABT'.