Règle à bords parallèles

Les constructions à la règle seule ne permettent pas grand chose.
Sauf si on accompagne cette règle d'autre chose : Par exemple un "traceur de parallèles" etc.
Un traceur de parallèles simple est d'utiliser une règle à deux bords parallèles, de largeur d.
Le "règlement" est alors :

• [C1] On peut tracer une droite par deux points connus.
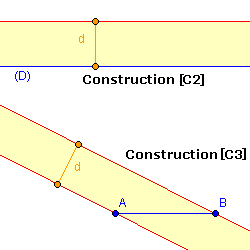
• [C2] On peut tracer une droite parallèle à une droite connue, à distance d = largeur de la règle.
• [C3] On peut tracer par deux points connus A et B une droite passant par A et une passant par B,
  parallèles et à distance d, si AB > d.
• Obtenir de nouveaux points par intersections de telles droites entre elles ou avec des droites connues.

Et c'est tout. On autorise toutefois le choix de points arbitraires, si le résultat de la construction ne dépend pas du choix de ces points ("tracer une droite quelconque" etc)

En utilisant les seules constructions [C1] [C2] [C3] ci-dessus construire :

• Une parallèle par un point donné à une droite donnée Indice
• Une perpendiculaire par un point donné à une droite donnée Indice

Peut-on se passer de la construction [C3] pour ces constructions là ? Indice

Plus compliqué : construire un triangle équilatéral ? un hexagone ? octogone ? dodécagone ? Indice
Un pentagone régulier ? décagone ? etc ? Indice
Même question : peut on se passer de l'axiome [C3] ? Indice

Détails