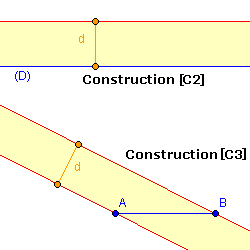
Règle à bords parallèles

Le "règlement" est :

• [C1] On peut tracer une droite par deux points connus.
• [C2] On peut tracer une droite parallèle à une droite connue, à distance d = largeur de la règle.
• [C3] On peut tracer par deux points connus A et B une droite passant par A et une passant par B,
  parallèles et à distance d, si AB > d.
• Obtenir de nouveaux points par intersections de telles droites entre elles ou avec des droites connues

Et c'est tout. On autorise toutefois le choix de points arbitraires, si le résultat de la construction ne dépend pas du choix de ces points ("tracer une droite quelconque" etc)

En utilisant les seules constructions [C1] [C2] [C3] ci-dessus construire :

Une parallèle par un point P donné à une droite (D) donnée [C4]

Tracer une droite PA quelconque.
Puis par l'axiome [C2] construire les parallèles à distances d et 2d de cette droite AP
La deuxième parallèle (la 3ème droite) coupe la droite (D) en C
PC coupe la droite médiane en I.    AI coupe la troisième droite en Q
PQ est la parallèle cherchée.

Preuve : les 3 parallèles équidistantes définissent I comme milieu de PC et I comme milieu de AQ. Par conséquent le quadrilatère PACQ ayant ses diagonales se coupant en leur milieux est un parallélogramme.
Dans l'applet, la largeur de la règle est définie par d déplaçable, la droite est définie par les deux points D et D' déplaçables, P déplaçable, La droite quelconque AP est définie par le point A déplaçable sur (D).

Cette construction n'utilise pas [C3]

Une perpendiculaire par un point donné à une droite donnée

Construction [C5] : Traçons une droite PA quelconque et la parallèle à distance d, coupant (D) en B
Par la construction [C3], on peut tracer l'autre paire de droite à distance d passant par A et B, qui est symétrique de la première par rapport à (D)
On opère de même avec un autre choix de droite PA'
Les deux symétriques passant par A et A' se coupent donc en P', symétrique de P par rapport à (D) et PP' est la perpendiculaire cherchée.
Dans l'applet, la droite est définie comme horizontale passant par A, sans perte de généralité. (P, A, A' et d déplaçables)

Cette construction peut servir aussi à construire le symétrique d'un point P par rapport à une droite.

Cette construction échoue si P est sur (D), mais alors une construction plus simple encore donne la perpendiculaire en P : [C5']
Traçons une droite quelconque par P et sa parallèle, coupant (D) en A
Traçons par [C3] la paire de droites passant par A et P et symétrique de la première, puis par [C2] une troisième parallèle à cette paire de droites.
Cette droite coupe la première parallèle en Q, et PQ est la perpendiculaire cherchée.
Dans l'applet, la droite est définie comme horizontale par P déplaçable, sans perte de généralité.
A est déplaçable sous la contrainte AP > d (sinon [C3] ne marche pas !) et définit la pente des droites arbitraires via [C3]

Preuve : les diagonales d'un losange sont perpendiculaires, et translations.

Autres constructions

• [C6] bisectrice(s)
  Construction évidente utilisant uniquement [C2]

  
  Les droites sont définies par les points bleus déplaçables.

• [C8] copie d'une distance
  La recopie d'une distance sur la même droite utilise uniquement les constructions [C2] d'une parallèle. et de simples droites [C1].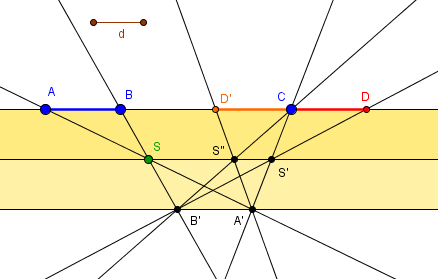

  
  La distance donnée AB est recopiée en CD via sa copie A'B' sur la parallèle à distance 2d, obtenue par deux fois [C2].
  L'échange de A' et B' donne CD' dans l'autre sens.
  A,B,C déplaçables ainsi que S quelconque sur sa parallèle (et d = largeur de la règle)
  La copie sur une droite parallèle revient à construire un parallélogramme, c'est à dire des parallèles via [C4].

  La copie sur une droite non parallèle se ramène sans perte de généralité à la copie de même origine O, en construisant le parallélogramme
  La copie s'effectue alors par une perpendiculaire à la bisectrice, perpendiculaire étant en fait une parallèle à l'autre bisectrice.

  

Ces constructions n'utilisent pas [C3], ce qui sera utile par la suite.
On peut de même effectuer toutes les constructions à la règle à un seul bord (c'est à dire [C1]) + parallèles sans utiliser [C3], une parallèle étant construite immédiatement par [C2], voire au besoin autant de parallèles quelconques par [C4], qui n'utilise que [C2].

• Milieu d'un segment, et de façon générale multiplication par p/q rationnel quelconque.
• Conjugué harmonique
• etc.

Voir la règle seule.

Ensemble des points constructibles

On va tout d'abord définir un repère du plan, et ce sans utiliser [C3]
Traçons deux droites quelconque et par [C2] leurs parallèles, définissant un losange ABCD
Les diagonales sont deux droites perpendiculaires, et par [C2] on peut définir un repère orthonormé OIJ, d'unité d

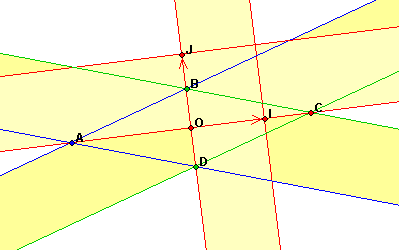
Sans utilisation de la construction [C3] on peut donc tracer des parallèles, des bisectrices et reporter des distances.
La règle à bords parallèles sans [C3] est donc équivallente à la règle à un seul bord et un bisecteur, ou un report de distances.
L'ensemble des points constructibles ainsi est un sous corps de R (pour les coordonnées dans le repère défini précédemment) et c'est même le plus petit sous corps pythagoricien de R.
Un corps K est pythagoricien si u et v étant dans K,  √u² + v² est dans K
Voir par exemple l'ouvrage de JC Carréga "Théorie des corps - La règle et le compas"
La caractérisation des points constructibles en autorisant [C3] semble plus compliquée. On peut déja se demander si cette construction est utile.

Suite