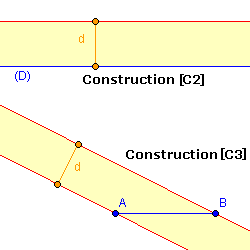
Règle à bords parallèles -suite

• [C1] Tracer une droite par deux points connus.
• [C2] Tracer une droite parallèle à une droite connue, à distance d = largeur de la règle.
• [C3] Tracer par deux points connus A et B une droite passant par A et une passant par B,
  parallèles et à distance d, si AB > d.

Rappelons le résultat provisoire :
L'ensemble des points constructibles sans [C3] est le plus petit sous-corps pythagoricien de R
Ce procédé est équivalant à la règle à un seul bord + le bissecteur (ou le transport de distances)
Nous allons maintenant examiner ce qu'apporte la construction [C3]

Utilité de la construction [C3] ?

Nous avons utilisé [C3] exclusivement pour construire des perpendiculaires.
La caractérisation précédente montre que l'on peut se passer de [C3] pour cela, puisque le report de distance ou le bissecteur suffisent !
Donnons un exemple d'une telle construction sans [C3] de la perpendiculaire en P à une droite donnée.

Sans perte de généralité, on peut supposer P sur la droite (sinon une parallèle à la droite par P ramène à ce cas)
Etape 1 : On trace tout d'abord deux perpendiculaires quelconques en P, en traçant deux losanges par la construction [C2] sur la droite donnée et sur une droite quelconque PX (X est déplaçable dans l'applet)

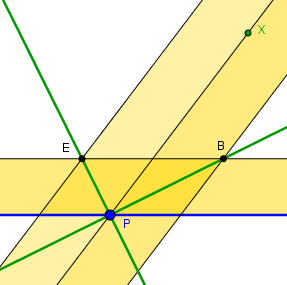
On obtient les droites PB et PE perpendiculaires.
Etape 2 : Sur ces droites, avec [C2] on construit deux carrés PRST et PTUV

Etape 3 : la droite RS coupe la droite donnée en D
Par des tracés de parallèles DD' // PR puis D'Q // TV on obtient le point Q avec UQ = SD
(détails des constructions des parallèles non montré, mais cela n'utilise que la construction [C2], voir précédemment)
La droite PQ est la perpendiculaire cherchée

Preuve : RD = VD' = TQ, les triangles PRD et PTQ sont donc égaux et se déduisent par une rotation de π/2

Par contre comme nous le verrons ultérieurement, [C3] est tout de même utile : il existe des constructions impossibles sans [C3], en d'autres termes on ne peut pas construire [C3] à partir de [C1] et [C2]

Donnons tout d'abord quelques exemples de constructions pratiques.

Triangle équilatéral

Il s'agit de construire  √3 = √1² + (√2)²
Ce qui n'offre pas de difficulté en construisant des perpendiculaires et en reportant la distance = 1 :
Sur le quadrillage de maille d, on construit OM = d√3 (par OM = d√2 et KM = d).
Puis on reporte OC = OM

La construction, ici réalisée sans utiliser [C3], peut être grandement simplifiée en utilisant [C3] :
On commence par construire AB = 2d en effectuant les deux premières étapes identiques (seuls A et B sont utiles, économisant une [C2] pour J,K inutiles)
On obtient alors immédiatement le triangle équilatéral par [C3] sur AB !
Sa taille est différente (hauteur = 2d au lieu de côté = 2d)
Pour obtenir un triangle d'une autre taille, il suffit de tracer des parallèles !
Nota : attention, le point S (étape 4) est bien l'intersection de MV et de la parallèle en U à OM à distance d.
Cette parallèle ne passe évidemment pas par J (car OJ = d), et S n'est pas sur JK.

Hexagone etc.

Par le tracé de bissectrices et le report de longueur sur cette bissectrice, on peut doubler le nombre de côtés d'un polygone régulier quelconque.
A partir du carré et du triangle équilatéral on obtient ainsi l'hexagone, l'octogone, le dodécagone etc tous les polygones réguliers de 2ⁿ ou 3.2ⁿ côtés.
Noter que l'hexagone peut ici s'obtenir encore plus rapidement en "dupliquant" des triangles équilatéraux par de simples tracés de parallèles !
Et même que si le triangle équilatéral de départ à pour hauteur 2d, les parallèles se tracent "instantanément" (par [C2] direct).
De toute façon, les bissectrices de l'hexagone sont obtenues "immédiatement" (BU)
Il n'y a plus qu'à reporter pour obtenir le dodécagone.

L'applet illustre le report de BD' = BD sur la bissectrice BU pour construire le dodécagone à partir de l'hexagone (A,B,d déplaçables)
E'F'G'A'C' se construisent de même, ou par de simples parallèles judicieuses à partir de D' et des sommets de l'hexagone,
Par exemple E' est l'intersection de la bissectrice de EBF (obtenue comme BU) et de la parallèle à DF par D'

Là aussi [C3] est inutile (sauf pour accélérer certaines constructions)

Pentagone régulier

La construction [C3] permet de construire θ, donc sin(θ) et tan(θ), à partir de cos(θ).
En fait à partir de AB = 1/cos(θ), mais comme l'ensemble des points constructibles avec [C2] seul est un corps,
la construction de 1/x à partir de x constructible est possible, sans même [C3].

Application au pentagone :
1/cos(π/5) = 4/(√5 + 1) = √5 - 1
ce qui se construit facilement.
L'angle de π/5 = 36° est donc constructible, et le pentagone s'en déduit par symétries et copie de distances
On commence par construire (déja vu, et pas re détaillé) le repère OIJ d'unité d = 1 (I déplaçable définit d dans l'applet)
Et les points à coordonnées U = (1,2) et V = (3,1) (par des [C2] répétés sur les axes)
OU et UV sont perpendiculaires et OU = d√5
La parallèle à distance d de UV par la construction [C2] donne le point A avec OA = d(√5 - 1) = d/cos(π/5)

La construction [C3] sur OA donne alors les angles cherchés, et l'angle au sommet du pentagone = 3π/5
Le pentagone est alors complèté par une simple construction [C2] !
En effet les distances de EB à CD et de BD à EA etc sont égales (le très connu nœud de la bande de papier)
Cela s'avère presque plus simple qu'un triangle équilatéral !
Pour obtenir une autre taille de pentagone, on trace des parallèles judicieuses (pour effectuer une véritable homothétie, sinon le pentagone n'est plus régulier)

Cette construction qui nécessite donc [C3] justifie à elle seule l'utilité de cet axiome.
Mais cette construction [C3] est encore plus puissante qu'il n'y paraît !

Cercles

Bien entendu on ne peut pas tracer de cercles !
Mais avec le report de distances on peut construire autant de points qu'on veut d'un cercle défini par son centre et un point : cercle "virtuel".

O et A déplaçables définissent le "cercle". X déplaçable définit la direction du point cherché A'
A' est construit comme intersection de la droite OX avec la droite AS, parallèle à IJ par A, donc perpendiculaire à la bisectrice OK de XOA
Même pas besoin de [C3] ...

Nous allons maintenant étudier les intersections de tels cercles (virtuels) définis par leur centre et un point.

Seconde intersection

Etant donné un cercle (virtuel) donné par son centre O et un point A, construire l'autre intersection d'une droite (D) passant par ce point
Sans même utiliser [C3], la construction est élémentaire :
Construire le point A' diamétralement opposé à A (copier OA' = AO)
La seconde intersection B cherchée est l'intersection avec la droite donnée de la perpendiculaire à cette droite issue de A'.
La construction détaillée de la perpendiculaire sans [C3] n'est pas détaillée (vue précédemment).
L'applet donne ici la construction simplifiée par [C3], via le symétrique A" de A' par rapport à la droite donnée.

O et A déplaçables définissent le cercle, X déplaçable définit la droite passant par A
S déplaçable est un point quelconque de la parallèle à OA

Axe radical de deux cercles

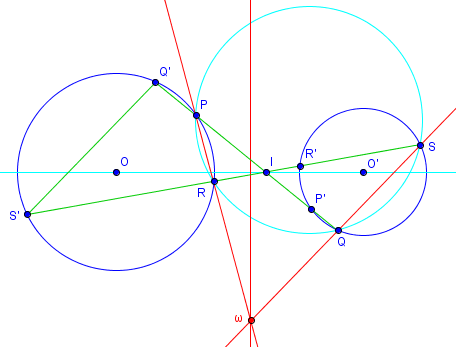Théorème :
Si P, Q sont antihomologues par rapport à un centre d'homothétie de deux cercles et si R et S sont antihomologues par rapport à ce même centre, les droites PR et QS se coupent sur l'axe radical des deux cercles
Preuve :
Les points Q' et S' sont homologues de Q et S, les triangles IQ'S' et IQS sont homothétiques de centre I et Q'S' est parallèle à QS
Les points "antihomologues" sont par définition les autres intersections de QQ' et SS' avec le cercle (O), c'est à dire P et Q sont antihomologues et de même R et S.
Les points P,R,S',Q' étant cocycliques, dans le triangle IQ'S', la droite PR est antiparallèle à la droite Q'S', donc à la droite QS, et par conséquent PQRS sont cocycliques.
La droite PR est donc l'axe radical des cercles (O) et (PQRS)
La droite QS est l'axe radical des cercles (O') et (PQRS)
Ces deux droites se coupent en, le centre radical de ces trois cerlces, donc sur l'axe radical de (O) et (O').

On peut alors appliquer ce théorème à la construction de l'axe radical de deux cercles (O, A) et (O', B) sans même utiliser [C3]
Deux parallèles quelconques passant par O et O' et le report des distances OA et O'B donnent les points P et Q' homologues sur les cercles (I est le centre d'homothétie)
La construction du deuxième point d'intersection avec (O',B) de la droite PQ' donne Q avec P et Q antihomologues.
La construction est répétée avec deux autres parallèles pour obtenir R et S
S' est obtenu comme intersection de la parallèle avec RI et non par report pour garder le même centre de symétrie ! en plus c'est plus simple que le report
S est la deuxième intersection de RS'
Les droites PR et QS se coupent en M sur l'axe radical donc.
L'axe radical est alors la perpendiculaire à OO' par M.

Dans l'applet, les points O,O', A et B déplaçables définissent les cercles
La première paire de parallèle est définie par P = A (pour simplifier)
La deuxième paire de parallèles est définie par r déplaçable.
Les constructions de parallèles, reports de distances, seconde intersection et perpendiculaire ne sont pas détaillées (voir ci-dessus).
(en vrai dans les applets ces constructions "vues précédemment" sont faites directement sans détailler non plus)

Poles et polaires

La polaire de P est la perpendiculaire à OP en P', P' étant le conjugué harmonique de P par rapport aux extrémités du diamètre BB',
Ces points B et B' sont constructibles par report de distance OB = OB' = OA sur la droite OP.
Le conjugué harmonique est constructible à la règle à un seul bord seule [C1]

Rappelons cette construction du conjugué harmonique :
Par un point S quelconque on trace les droites SP, SB et SB'
Par un point I quelconque de la droite SP, on trace les droites IB et IB' qui coupent SB et SB' en M et M'
La droite MM' coupe OP en P', conjugué harmonique de P par rapport à BB'.
Dans l'applet, O et A déplaçables définissent le cercle, P déplaçable.
S et I déplaçables définissent les droites quelconques utilisées.

Le pole d'une droite est inversement le conjugué harmonique du pied de la perpendiculaire à la droite donnée par O.

Utilisation de [C3] : intersection de deux cercles particuliers

La construction [C3] est exactement la construction de l'intersection du cercle de diamètre AB et du cercle de centre B de rayon d : la perpendiculaire issue de B à la droite tracée par [C3] passant par A coupe cette droite en M, intersection des deux cercles.
C'est d'ailleurs ainsi qu'est simulée [C3] dans les applets, en l'absence d'une bonne règle en bois dans Java...
Pour construire l'intersection de deux cercles quelconques, l'un étant centré sur l'autre, on opère une homothétie (par de simples parallèles et Thalès, [C2] uniquement), on "redimensionne" la figure pour avoir le rayon du cercle (O') = d
On applique alors [C3] directement, puis on effectue l'homothétie inverse (deux simples parallèles) pour obtenir le point d'intersection des deux cercles donnés.

Les points O et O'' déplaçables définissent le premier cercle, R déplaçable définit le second cercle. de centre O'.
On trace la droite OO', et on reporte OB = OO' pour obtenir le diamètre BO'
On reporte O'A = O'R
Construire alors (pas détaillé mais déja vu) la perpendiculaire en O' à OO',
et tracer les parallèles à distance d de OO' et de cette perpendiculaire pour obtenir FD = d
Le centre d'homothétie envoyant O'A sur FD est construit : point S intersection de O'F et AD.
L'homothétique de B est tracé : intersection E de SB avec FD.
On a ainsi "redimensionné" les données en :
  « construire l'intersection des deux cercles roses, celui de diamètre EF et celui de centre F et de rayon FD = d »
Ce qui se fait instantanément par la construction [C3] de la règle sur E,F.
L'homothétie est inversée en traçant la parallèle à cette règle EP' par B et la perpendiculaire en O' (alias parallèle à FP') qui se coupent en P, homothétique de P' (sans qu'il soit nécessaire de tracer effectivement P' d'ailleurs)
Les tracés de parallèles et de perpendiculaires, déja vus, ne sont pas détaillés.

Intersection d'une droite et d'un cercle

Construisons le pole de la droite comme vu précédemment.
Les intersections cherchées sont alors les intersection du cercle donné avec le cercle de diamètre OP, par la construction précédente.

Intersection de deux cercles

Construisons l'axe radical des deux cercles, puis l'intersection de l'un d'eux avec cet axe radical

Ces constructions sont la répétition des constructions précédentes, et je ne fournis pas d'applet : une applet détaillée donnerait une construction filandreuse, et sinon cela n'apporte rien de plus.

Conclusion étonnante

On vient de voir comment, avec l'aide de la construction [C3], la règle à bord parallèle permet de construire des intersections de cercles entre eux ou avec des droites. La conclusion en est que :

La règle à bords parallèles seule permet toutes les constructions de points et de droites constructibles à la règle et au compas

Mais dans la pratique c'est bien sûr inutilisable, à cause de la complexité des constructions.
Le compas, ou son équivalant dans les logiciels, a encore de beaux jours devant lui...