Centres de deux cercles non sécants

La construction à la règle seule des centres de deux cercles sécants [resp. tangents, concentriques] est tout compte fait relativement simple.
Hermite et Cauer ont montré (1912) que la donnée d'un seul cercle ou de deux cercles non sécants (sans leur centre) ne suffit pas.
Christian Gram a alors prouvé (1956) qu'il est possible de construire leur centre étant donné un seul point A de la ligne des centres.
Cette construction est particulièrement complexe. Elle utilise les notions et constructions suivantes.

Mais tout d'abord déterminons la ligne des centres, ce qui est assez simple.
Construisons les polaires de A par rapport à ces deux cercles
Ces droites sont parallèles (toutes deux perpendiculaires à la ligne des centres) et permettent donc de tracer autant de parallèles à celles-ci que l'on veut, en particulier une sécante à l'un des cercles donnés, et le milieu de cette corde.

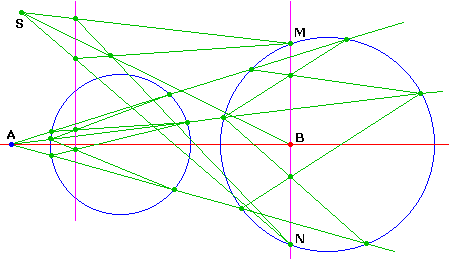
Ici A est en dehors d'un des cercles au moins, de sorte que la polaire coupe déja le cercle sans qu'il soit besoin de tracer une parallèle supplémentaire.
Les polaires ont été tracées par trois sécantes issues de A, pour obtenir une meilleure précision du tracé et des points "pas trop loin", en n'utilisant que les diagonales intérieures.
Le point auxilliaire S pour la construction du milieu B de MN peut tout aussi bien être en A, choisi ici excentré pour "aérer" le tracé.

Involution de Desargues

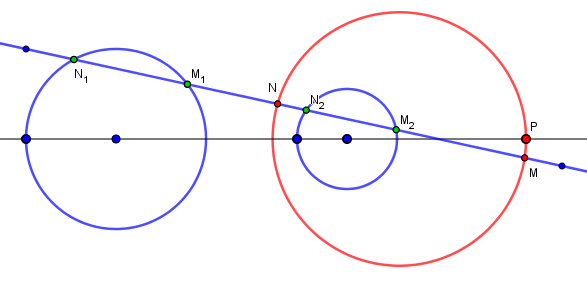
Les deux cercles donnés définissent et font partie d'un faisceau (de coniques qui sont toutes des cercles)
Les intersections d'un cercle de ce faisceau avec une droite fixe d définissent sur cette droite une involution, appelée involution de Desargues.
Chaque cercle du faisceau définit un couple de points homologues M,N dans cette involution. (Les points M et N peuvent être imaginaires)
Une telle involution sur une droite est parfaitement définie par la donnée de deux couples de points homologues (M1,N1) et (M2,N2), intersections de d avec les deux cercles donnés.
Cette involution M↔N est mise en évidence dans l'applet ci-dessous.
Le point P choisit le cercle variable du faisceau (construit comme l'unique cercle du faisceau passant par P)
Les points bleus définissent les cercles donnés et la droite d.

Points fixes d'une involution

L'involution étant définie par deux couples de points homologues.
Lorsque l'involution est "hyperbolique", elle possède deux points fixes réels.
Ici c'est le cas, et ces deux points fixes sont les points de contact des cercles du faisceau tangents à la droite donnée.
De façon générale, étant donné un cercle quelconque, sans même connaître son centre, il est possible de projeter cette involution de la droite sur le cercle.
Les droites joignant deux points homologues de l'involution sur le cercle passent par un point fixe : le pôle Q de l'involution (théorème de Fregier).
Les points fixes de l'involution sur le cercle sont alors de toute évidence les points de contact des tangentes issues de Q, c'est à dire les intersections de la polaire de Q avec le cercle, construite ainsi "comme d'hab" par les intersections I et J des diagonales (cette polaire est appelée l'axe de l'involution).
Il suffit de reprojeter l'involution sur la droite pour obtenir les points fixes U, V de l'involution sur cette droite.
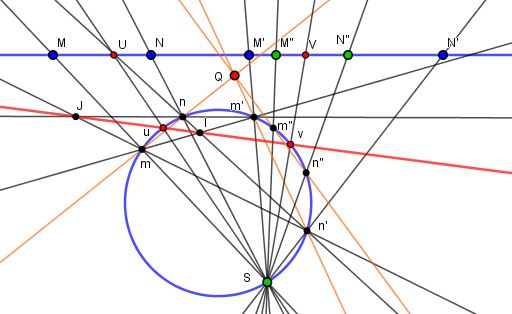
L'applet ci-dessous montre cette construction.
Le centre S de la projection est déplaçable et montre bien que U et V sont indépendants du choix de S
L'involution sur d est définie par les points M↔N et M'↔N' déplaçables.
On peut d'ailleurs définir ainsi une involution non hyperbolique : elliptique pas de point fixe réel, ou parabolique un seul point fixe réel.
Le point vert M" est déplaçable, l'applet construisant le point homologue N" dans l'involution.

Points d'un cercle non tracé d'un faisceau

L'étape suivante de la construction consiste, ayant déterminé un cercle du faisceau tangent à d par son point de contact U, à obtenir quelques autres points de ce cercle (sans compas, on ne peut pas le tracer).
Choisissons une droite quelconque δ passant par U et coupant les cercles donnés.
Ces cercles définissent sur cette droite une involution et le second point d'intersection de δ avec le cercle à construire est alors l'homologue de U dans cette involution.
La construction se fait comme dans l'applet ci dessus pour construire N" à partir de M" : U est projeté en u sur le cercle donné, l'homologue u' de u sur ce cercle est obtenu comme second point d'intersection de uQ, et on reprojette sur la droite en U'.
Le cercle de projection étant le cercle donné Γ du faisceau, les points M et N sont inchangés dans la projection, et la droite mn est la droite δ, même si M et N sont imaginaires ! Q est donc l'intersection de m'n' avec δ.
Ceci permet de construire des points du cercle même si δ ne coupe pas le premier cercle !
Par contre il faut que m', n' soient réels et que δ coupe effectivement l'autre cercle Γ' du faisceau.
Si U est extérieur au cercle Γ', on ne peut alors obtenir que des points sur une petite partie du cercle cherché.
Dans le cas qui nous intéresse, U et V sont intérieurs aux cercles donnés, on obtient donc tous les points que l'on veut, sans limitation.
La construction est valable pour tout point U et tout faisceau de cercle.
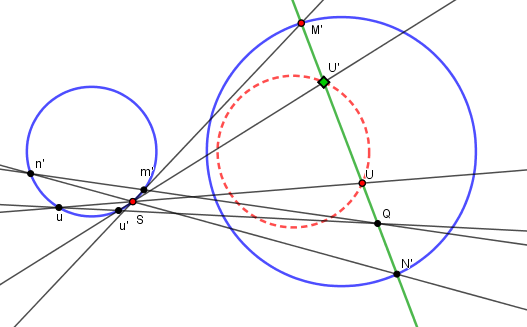
Dans l'applet ci-desous, les cercles Γ et Γ' peuvent être modifiés par les points bleus.
Le centre de la projection S est déplaçable. Bien sûr U aussi, et le point courant M' (la droite δ).
La précision pratique des tracés est déplorable car les droites sont définies par des points très proches. Cela ne gène pas l'applet, mais un véritable crayon si.
La position de départ de l'applet est avec M et N imaginaires. On peut les faire apparaître en déplaçant M'.

Cercle défini par 5 points

Ayant ainsi défini 5 points UBCDE du cercle tangent en U, il s'agit maintenant de construire l'intersection de ce cercle et d'une droite quelconque (en fait la ligne des centres). Avant cela, donnons déjà la construction de la polaire de M par rapport à ce cercle dont on ne connaît que 5 points.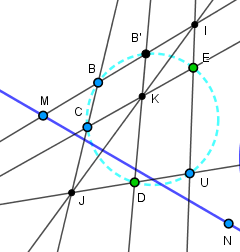
En fait, à partir de ces 5 points on peut construire facilement les secondes intersections de droites passant par un point connu du cercle à l'aide du théorème de Pascal.
La construction de la polaire est alors "comme d'hab", en choisissant comme sécantes arbitraires les droites MB et MC, mais en intercallant deux fois la construction de Pascal pour obtenir B' et C' :
MB coupe EU en I
BC coupe DU en J
IJ coupe CE en K
DK coupe MB en B'
Et de même pour C'
La polaire est alors la droite joignant les intersections BC∩B'C' et BC'∩B'C

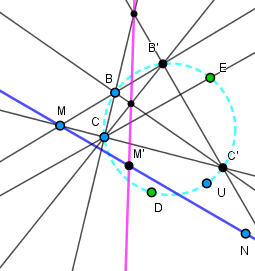
On est alors prêt pour construire l'intersection avec une droite d quelconque.
Choisissons deux points M et N sur d et construisons leur polaires, coupant d en M' et N'.
L'involution définie sur d par M↔M', N↔N' est en fait la conjugaison harmonique par rapport aux points d'intersection P, Q cherchés.
Ces points sont donc les points fixes de cette involution, que l'on construit comme d'habitude en la projetant sur un des cercles donnés.

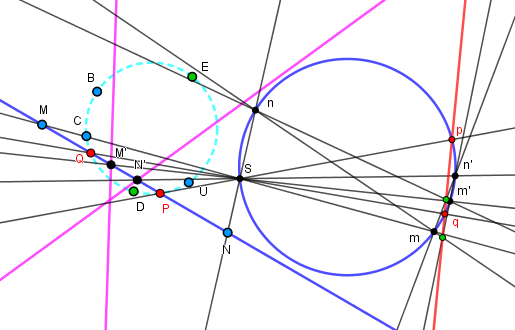
L'applet suivante montre cette construction, le cercle donné (tracé) est en bleu.
Le cercle non tracé (cyan) est défini par les points déplaçables U, B, C et les points D, E dessus
M et N sont déplaçables et définissent la droite d.
Le point S déplaçable est le centre de la projection. La construction échoue si S est sur la droite MN.

Résumé

La construction complète à la règle seule du centre de deux cercles non sécants donnés sans leur centre, étant donné un point A quelconque de la ligne des centres, est ainsi :

1. Déterminer la ligne des centres en construisant les polaires de A, et ainsi le milieu d'une corde parallèle à ces polaires, c'est à dire perpendiculaire à la ligne des centres.
2. Tracer une droite d quelconque coupant les deux cercles et définissant une involution hyperbolique.
   Projeter cette involution sur l'un des cercles et en déterminer les points fixes U et V.
   Ceci définit les points de contact U et V des cercles du faisceau tangents à d.
3. Construire 4 autres points sur le cercle du faisceau passant par U,
   en utilisant les involutions induites sur 4 droites δ passant par U, projetées sur un des cercles.
4. Construire les intersections de ce cercle défini par 5 points avec la ligne des centres.
5. Recommencer avec le cercle tangent en V.
6. Les diamètres ainsi définis donnent avec les points U et V deux couples de droites parallèles.
   (U et V sont homologues dans l'homothétie entre les deux cercles tangents, donc UP // VP')
   Ce qui permet de tracer un autre diamètre des cercles donnés, et donc leur centre comme intersection avec la ligne des centres.

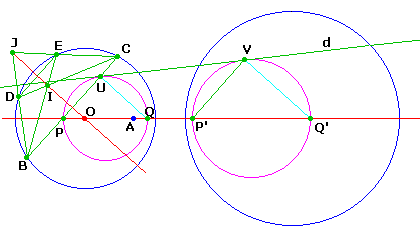
Euh... quelques centaines de droites à tracer... courage.
(je n'ai pas celui d'écrire l'applet complète, combinaison de plusieurs copies des applets ci-dessus)