Partage du champ - Solution

Le puits est sur un côté - partage en deux

Si P est sur un sommet, disons C, la médiane issue de C donne la solution et M est le milieu du côté opposé.
Si P est au milieu d'un côté, la médiane convient aussi et M est le sommet opposé.
Dans le cas général, désignons par C le sommet le plus proche de P sur le côté BC. Alors le point M sera sur le côté AB.
La surface du triangle ABC est 1/2 BA.BC.sinB et la surface de PMB est 1/2 BM.BP.sinB. Le partage du champ sera équitable si BM.BP=1/2 BC.BA.
Une construction possible : Soit H le milieu de BC. La parallèle à PA passant par H coupe AB en M.
Les triangles BPA et BHM étant semblables, BP/BH = BA/BM soit BP.BM = BH.BA = 1/2 BC.BA.

Le puits est sur un côté - partage en trois

S'il y a trois frères le principe est le même, mais il faut tout d'abord déterminer à partir de quel sommet(s) effectuer la construction.
Les points particuliers suivants vont permettre de préciser les différents cas selon la position de P sur le segment BC.
Appelons C' et C" les points au tiers de AB et K au milieu et de même sur les autres côtés.
Si P est en C les droites CC' et CC" sont solution (1/3 de la base AB)
Si P vient en A", au tiers de BC à partir de C, AA" est solution et l'autre droite est telle que BM.BP=BM.2/3BC=1/3BC.BA et donc BM=1/2BA,
M est en K au milieu de BA.
Si P vient en H milieu de BC, le calcul précédent montre que les droites HB' et HC' sont solution. Conclusion :

• Si P est au premier tiers de BC à partir de C (parcourt le segment CA"), les deux points M et N sont sur AB (parcourent respectivement C'A et C"K), BM.BP=2/3BC.BA=BA".BA et BN.BP=1/3BC.BA soit BN=1/2BM. Les deux points se constuisent à partir de B.
• Si P est entre le premier tiers et la moitié de BC à partir de C (parcourt le segment A"H),
  M est sur AC (parcourt AB') et N sur AB (parcourt KC').
  CP.CM=1/3CB.CA=CA"CA construit M à partir de C.
  BP.BN=1/3BC.BA=BA'.BA construit N à partir de B.
• Etc... par symétrie sur les autres parties des côtés du triangle.

Le puits est dans le champ - Partage en deux

Lorsque P parcourt le segment HC, l'enveloppe de MP est un arc d'hyperbole tangente aux médianes AH et CK en leur milieu, et limité par ces points. Les asymptotes sont les côtés AB et BC.
En échangeant le rôle du puits P et du point M, c'est le même arc d'hyperbole quand P parcourt AK.
Quand P parcourt ainsi les trois cötés du triangle, l'enveloppe de MP est un ensemble {H} de trois arcs d'hyperboles. Cette remarque va nous permettre de résoudre le cas où le puits P est à l'intérieur du triangle ABC :
Il s'agit alors de chercher une tangente à {H} issue de P. Il y a trois solutions si P est à l'intérieur du triangle curviligne délimité par {H}, une seule sinon. L'arc d'hyperbole concerné dépend alors de la région (1,2 ou 3) où se trouve le puits P.

Une construction géométrique (à la règle et au compas) de cette tangente est relativement compliquée.
Supposons par exemple P dans la région (1), il s'agit alors de construire la tangente à l'hyperbole de centre A.
Nous allons tout d'abord caractériser l'hyperbole par son foyer F et son cercle principal (C).
Une tangente à l'hyperbole passant par P est alors obtenue en cherchant un triangle UFP rectangle en U, avec U sur le cercle principal (C). UP est tangente à l'hyperbole.

Construction du foyer et du cercle principal

Construire C' sur AC tel que AC' = AK = 1/2 AB. Le cercle de diamètre AC et la perpendiculaire en C' à AC se coupent en J et AJ² = AC.AC' = 1/2 AB.AC. Le cercle de centre A de rayon AJ coupe AC et AB en R et S ainsi que la bissectrice de l'angle A en F. AF coupe RS en I. Le cercle de centre A de rayon AI est le cercle principal (C) de l'hyperbole, F le foyer et I le sommet.

Construction de la tangente issue de P

On peut alors construire les tangentes à l'hyperbole passant par un point P (le puits).
Le cercle de diamètre PF coupe (C) en U et V, U à l'intérieur du triangle BGC (G centre de gravité).
PU est la tangente cherchée

Note : PV est aussi une tangente mais le point de contact est au delà des limites de l'arc de {H}.
Si P n'est pas dans une région (1) il faut choisir une autre hyperbole ! Un cas particulier est le cas où P est dans le triangle curviligne délimité par les médianes GB et GC et l'arc de {H}. Alors les deux points U et V conviennent et donnent quand même deux solutions avec cette hyperbole-ci, en plus de la tangente à l'hyperbole de la région 2 ou 3.

Autre méthode

Une méthode plus directe :
Choisisons tout d'abord comme ci dessus le sommet A à partir duquel effectuer la construction. C'est à dire selon la zone, délimitée par les médianes, dans laquelle se trouve le puits.
Les parallèles à AB et AC issues du puits coupent AB en U et AC en V.
Posons AU = u, AV = v, AM = x, AN = y. On a alors :
x.y = b.c/2 comme ci-dessus, et avec les triangles semblables AMN et UMP : y/v = x/(x-u)
En éliminant y entre ces deux équations on obtient 2.v.x² = b.c.(x-u) ou encore en posant p = b.c/(2.v) :

 x² - p.x + p.u = 0  [1]

Construisons AQ = p = b/2 × c/v = AK × AB/AV :
La parallèle à BV issue du milieu K de AC coupe AB en Q.

Une perpendiculaire en U à AB coupe le cercle de diamètre AQ en W : AW² = AU.AQ = p.u

Une parallèle à AB à la distance AH = AW de AB coupe le cercle en X₁ et X₂ qui se projettent en M et M' sur AB.
OM² = OX² - MX² = p²/4 - p.u

Par conséquent AM et AM' sont les solutions de l'équation [1].
Le point M' ne convient pas car M'P coupe AC au delà de C.

Dans le cas où P est à l'intérieur du triangle curviligne {H}, le choix du sommet opposé (B au lieu de A) donne avec une construction similaire les deux autres solutions. Si la parallèle à la distance √(p.u) ne coupe alors pas le cercle, c'est que P est à l'extérieur du triangle curviligne et il n'y a qu'une seule solution.
Enfin le sommet A étant choisi, on peut effectuer une construction symétrique donnant la (les) mêmes solution(s) en choisissant C au lieu de B, ce qui donne AN = y au lieu de AM = x.

nota : la construction, précédente ne marche que si u et v sont "positifs"
une construction meilleure (marche pour P n'importe où dans la région rosée du plan limitée par les médianes et l'arc d'hyperbole)

Le puits est dans le champ - Partage en trois

Le partage en trois est indéterminé. Déplaçons le point M sur le segment AC. L'aire de AMPN varie de façon continue de S et l'aire de MPLC varie en même temps de -S. On peut alors déplacer L sur BC (ou au delà, sur le pourtour du champ) pour que l'aire de MLPC varie de +S, et N sur AB (ou au delà, sur le pourtour du champ) pour que l'aire de AMPN varie de -S. On obtient ainsi une autre solution.

Conclusion : la position de M sur AC est arbitraire, quel que soit le choix de M on peut toujours trouver L et N sur le pourtour du champ pour le partager en trois parties égales.

Note : Le partage en deux en admettant un angle au niveau du puits est pour les mêmes raisons indéterminé et donc sans intérêt. Quoique...
Donc un champ ABC avec un puits P en plein dedans et un chemin MP menant du côté AC au puits. Les deux frères veulent se partager le champ par une droite Px recoupant la lisière du champ quelque part en N. Construire N.

On peut sans perte de généralité supposer MA>MC et Aire(ABC)=1. On a alors trois cas :

1. Aire(PMA)>1/2 : le point N est sur MA. Sinon :
2. Aire(PMA)+aire(PAB)>1/2) : le point N est sur AB. sinon :
3. Aire(PMA)+aire(PAB)<1/2) : le point N est sur BC

Mais pour construire... à vous de jouer. Na !
Indice : construire judicieusement x=a*b/c avec Thalès.

Pour trois frères on peut de même construire N et L avec ABC, P, M donnés.
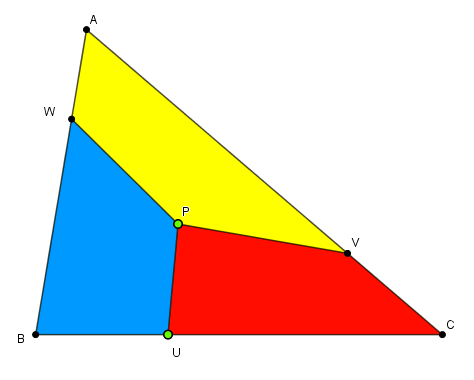
Une applet, avec L,M,N renommés en U,V,W :
Le point P est restreint à l'intérieur de ABC (sinon la construction serait aberrante, avec des morceaux d'aire négative)
U est déplaçable sur BC. Les cas où aucune extrémité n'est sur BC se traitent en renommant les sommets : il y a au moins un côté sur lequel il y a au moins une extrémité, c'est sans perte de généralité "U sur BC".

L'applet utilise des constructions conditionnelles pour distinguer les différents cas de figure.
Le critère est obtenu en comparant les aires PUC, PAC, PAB et ABC :

1. PUC ≥ ABC/3, V sur UC : UV/UC = [ABC/3]/PUC
2. ABC/3 - PAC ≤ PUC < Aire(ABC)/3, V sur AC : CV/CA = [ABC/3 - PUC]/PAC
3. ABC/3 - PAC - PAB ≤ PUC < ABC/3 - PAC, V sur AB : AV/AB = [ABC/3 - PUC - PAC]/PAB
4. ABC/3 - PAC - PAB > PUC, V sur BU : BV/BU = [ABC/3 - PUC - PAC - PAB]/PUB

Une construction géométrique peut être obtenue en construisant des triangles équivallents par des parallèles.
Le point W est construit de l'autre côté par une méthode similaire.

Annexes

Si on considère des aires algébriques pour les quadrilatères AVPW, BWPU, CUPV, d'aires égales, avec U,V,W sur les droites supports respectifs de BC,AC et AB, on peut chercher pour quel point P les différentes positions de U,V,W forment un triangle toujours semblable.
Sans entrer dans les détails, P est alors à l'un des foyers de l'ellipse de Steiner inscrite dans ABC.

Une autre question intéressante est de construire un point P tel qu'on puisse trouver PU_|_BC, PV_|_AC et PW_|_AB, c'est à dire que le triangle podaire UVW de P permette de diviser par PU,PV,PW le champ ABC en 3 aires égales...
solution