n-gone effacé - solution

J'ai tracé un polygone régulier à n côtés (un n-gone) sur le sable. Sur chacun de ses côtés j'ai placé une pierre.
Deux jours après, les pierres n'ont pas bougé de place, mais le n-gone est effacé.
Sauriez vous retrouver le tracé du n-gone ?

En fait le problème est sur-spécifié car avec seulement 4 des n pierres, il est possible de reconstruire le n-gone
Par exemple la reconstruction du pentagone ABCDE, étant données les pierres PQRS sur les côtés AB, BC, CD et AE.

L'angle au sommet d'un pentagone est π - 2π/5 = 3π/5.
Le point A est donc sur le cercle d'où on voit le segment PS sous l'angle 3π/5.
Son centre M est tel que SMP = 4π/5 ou encore PSM = SPM = π/10
Ces angles étant constructibles, le point M est constructible.

La diagonale AC forme avec le côté AB un angle de π/5.
Elle coupe le cercle en I et l'angle PMI = 2×PAI = 2π/5.
Le point I est donc parfaitement déterminé par la seule donnée des points P et S.

De la même façon on construit le cercle d'où on voit RQ sous l'angle 3π/5, avec RQN = QRN = π/10, puis le point J sur ce cercle avec QNJ = 2π/5.
La diagonale du pentagone est donc la droite IJ, qui recoupe les cercles en A et C.
On complète le pentagone en traçant AP et CQ qui se coupent en B. Puis en reportant AE = AB sur la droite AS et CD = CB sur la droite CR.

L'affaire n'est pas aussi simple si I et J sont confondus, mais alors il y a une infinité de solutions et n'importe quelle droite passant par I = J et coupant les deux cercles fait l'affaire.
On peut alors chercher le plus grand pentagone : Le point B est sur l'arc d'où on voit PQ sous l'angle 3π/5, de centre O avec PQO = QPO = π/10.
La double sécante APB est alors maximale quand AB // MO.

Enfin si PQRS sont donnés à priori (et non pas sur un pentagone effacé), il est possible que le problème soit insoluble, c'est à dire que les points PQRS ne soient que sur les prolongements des côtés du pentagone.
S'il ne reste effectivement que 4 pierres et si on ne sait pas sur quels côtés elles étaient, il y a à priori 5 solutions pour le choix du côté où la pierre a disparu.

Cercles 

Les "points" peuvent aussi avoir "une épaisseur", c'est à dire être des cercles (construire un carré dont les côtés sont tangents à quatre cercles donnés)

Une simple translation parallèlement aux côtés du carré, de module le rayon des cercles (O1) et (O2) transforme le problème en chercher un carré abcd, dont les côtés passent par O1 et O2 et sont tangents aux cercles de centre O3 de rayon r1+r3, et de centre O4 de rayon r2+r4.
La technique déja vue de rotation du carré de 90° conduit alors à construire O2O'3 = O1O3 et perpendiculaire à O1O3, et de tracer le cercle de centre O'3 égal à celui de centre O3 (de rayon r1+r3)
Le côté ad est alors la tangente commune aux deux cercles de centre O4 (de rayon r2+r4) et O'3
Les rotations et translations sont alors opérées en sens inverse pour obtenir le carré ABCD.
On répète la construction pour les autres possibilités (permutations des cercles, perpendiculaire dans l'autre sens et autres tangentes communes) pour obtenir diverses variantes où les cercles sont tangents aux prolongement des côtés, ou à l'extérieur du carré. Ces autres solutions ne sont pas indiquées dans l'applet.

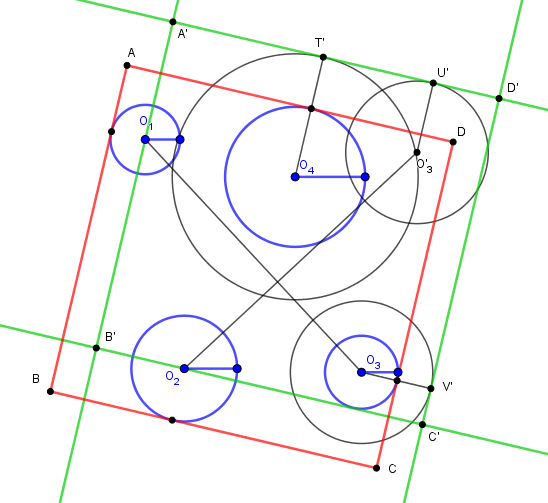
Les points bleus déplaçables définissent les centres et rayons des quatre cercles.
La construction simplifiée de la tangente commune utilisée dans l'applet échoue si les cercles (O4) et (O'3) ont même rayon r2+r4 = r1+r3.
(la construction fiable à tout coup des tangentes communes dans une applet est trop compliquée, na)

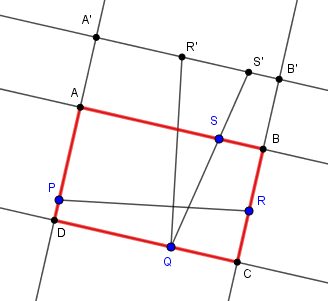
Rectangles 

Etant donnés quatre points, construire un rectangle de forme donnée passant par ces quatre points. Par exemple un rectangle d'or.

A vous de jouer...
Indice
Solution détaillée