Carré effacé II - solution

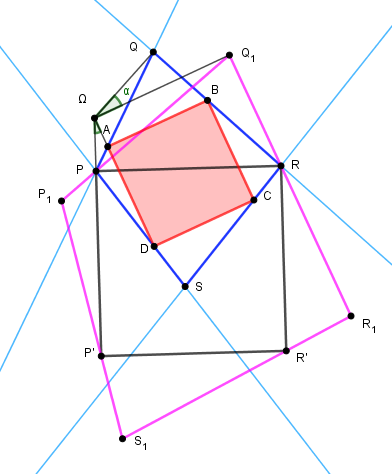
Etant donné un quadrilatère PQRS quelconque, construire un carré ABCD, A sur PQ, B sur QR, C sur RS et D sur SP.

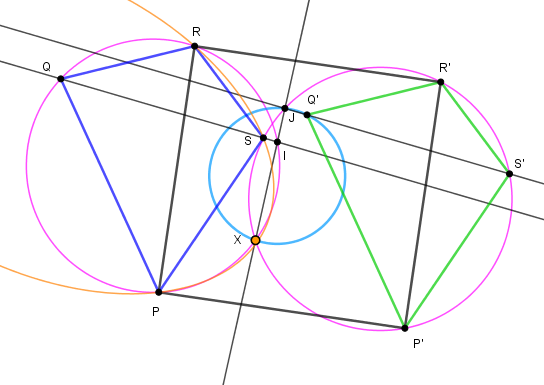
Construire sur PR un carré PRR'P' et le quadrilatère P'Q'R'S', translaté de PQRS.
Tracer les cercles circonscrits à PQR et P'R'S'. Les droites SQ et S'Q' recoupent ces cercles en I et J.
La droite IJ recoupe ces cercles en Q₁ et S₁.
Q₁P et S₁P' se coupent en P₁, Q₁R et S₁R' en R₁.

Les angles inscrits PQ₁I = PQI et P'S₁J = P'S'j montrent que les triangles P₁Q₁S₁ et PQS sont semblables. De même S₁Q₁R₁ et SQR, avec le même rapport de similitude S₁Q₁/SQ. Les quadrilatères P₁Q₁R₁S₁ et PQRS sont donc semblables et on a ainsi construit un carré PRR'P' inscrit dans un quadrilatère P₁Q₁R₁S₁ semblable au quadrilatère donné PQRS.

Il "suffit" de construire le transformé de PRR'P' dans la similitude P₁Q₁R₁S₁ → PQRS pour avoir le carré cherché.

Construisons tout d'abord le centre de similitude de S₁Q₁ → SQ. Ces deux droites se coupent en I, et le centre de similitude est sur le cercle circonscrit à IQQ₁, déjà tracé.
Le centre de similitude Ω est la seconde intersection de ce cercle et du cercle ISS₁
Le rapport k = ΩQ/ΩQ₁ et l'angle α = (ΩQ₁ ; ΩQ)
Il ne reste plus qu'à construire A par ∠PΩA = α et de même pour les autres sommets du carré ABCD.

Nota : Les angles se construisent facilement via les arcs égaux à Q₁Q sur le cercle (PQR), et le rapport est "automatique"

Une applet pour montrer cette construction à partir d'un quadrilatère quelconque PQRS dragable.
Les sommets ABCD du carré peuvent ne pas être sur les côtés même du quadrilatère PQRS, mais sur leur prolongements.
Le carré avec ses sommets sur les extensions peut devenir très grand, en particulier si PQRS est un rectangle !

Comme vous pouvez le constater, il y a pas mal de "hoquets" où la construction précédente échoue. Ceci se produit lorsque P1,Q1,R1,S1 sont confondus : la similitude a alors un rapport infini, et le carré une taille infinie aussi, c'est à dire que le problème n'a pas de solution.
C'est le cas pour un rectangle déja signalé, mais pas seulement.

La construction échoue aussi si les points I et J sont confondus, la droite IJ est alors indéterminée et il y a une infinité de solution.
C'est le cas où PQRS est un carré, mais pas seulement.

Ci-dessous une applet qui construit un quadrilatère PQRS admettant une infinité de solutions.
A partir de PQR déplaçables, l'applet construit S (comment ? solution le mois prochain, na)
Le bouton anim permet de voir l'infinité de carrés "inscrits" dans ce quadrilatère.
On peut en choisir un en pause en déplaçant le point pilote blanc (un point quelconque du cercle circonscrit à PQR)

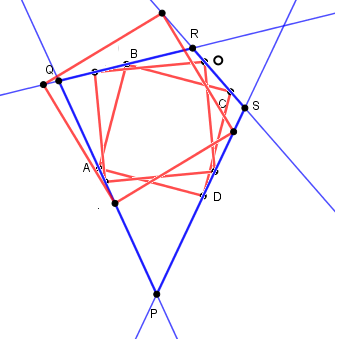
Déterminer comment l'applet construit S revient à trouver un critère déterminant quand PQRS admet une infinité de solutions.

Inversement déterminer les cas d'impossibilité où la construction échoue car le quadrilatère abcd est de taile nulle, soit les cas où a=b=c=d
Etant fixés P Q R arbitraires, et donc le carré PRrp.

Soit a=b=c=d un point du cercle circonscrit à PQR (point 'b' de ce cercle)
Il est commun (point 'd') au cercle circonscrit à rps et ce cercle est donc tracé comme cercle circonscrit à arp
La droite aIJ coupe ces cercles en I et J et QI est parallel à qj
Les angles de ces droites avec aIJ sont donc égaux et le point J est sur le cercle d'ou on voit aq sous le même angle que l'on voit aQ depuis le cercle (PQR)
Le point J est donc déterminé, et donc le point s, seconde intersection de Jq avec le cercle (arp), puis S par la translation pqrs → PQRS

Le lieu de S pour PQR donné en faisant varier a sur le cercle (PQR) est une conique ?
On remarque que le point S défini par PQR donnant une infinité de solutions est sur ce lieu : parmi l'infinité des solutions se trouvent la "solution" de taille infinie, c'est à dire correspondant à a=b=c=d. I=J est alors l'autre point d'intersection des cercles (PQR) et (rps)