Triangles - Solutions

Construire un triangle ABC connaissant ...

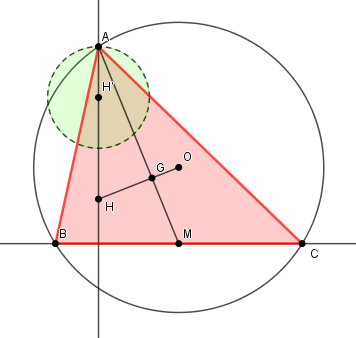
Un sommet A, l'orthocentre H et le centre de gravité G

Le milieu M de BC est facile à construire : GM=AG/2. La droite BC est alors la perpendiculaire à AH de M.
Les points O, G et H sont alignés (droite d'Euler) et GO=HG/2.
Le cercle circonscrit, de centre O et passant par A coupe la droite BC en B et C.

Discussion :
La solution existe si la perpendiculaire coupe le cercle circonscrit.
OM=AH/2, et donc le rayon OA du cercle circonscrit doit être > AH/2.
Pour A et H donné le lieu de O est donc l'extérieur du disque de centre A de rayon AH/2.
Comme G est l'homothétique de O de centre H de rapport 2/3, le lieu de G est l'extérieur du disque de diamètre 2/3 AH.