Triangles - Solutions

Construire un triangle ABC connaissant ...

Un sommet A, le centre du cercle circonscrit O et le centre du cercle inscrit I

On peut construire ABC en utilisant la formule due à Euler : OI² = R² - 2Rr où R est le rayon du cercle circonscrit et r le rayon du cercle inscrit. Il est alors facile de construire r avec r = (R+OI)(R-Oi)/R soit r/(R-OI) = (R+OI)/R
On construit ainsi le cercle inscrit, puis les tangentes issues de A coupent le cercle circonscrit en B et C.

Mais ... quelques propriétés remarquables :
Soit J le centre d'un cercle exinscrit dans l'angle A. Le milieu de IJ est sur le cercle circonscrit, et le cercle de diamètre IJ passe par B et C. Le milieu de IJ est bien sûr sur la bissectrice ! C'est donc l'intersection de la bissectrice avec le cercle circonscrit.

Ceci donne une construction bien plus simple :
La médiatrice de AI coupe le cercle circonscrit (de centre O et passant par A) en P et Q. PI est la bissectrice de l'angle B et coupe le cercle en B. De même QI coupe le cercle en C.

Mais il y a encore plus simple : AI coupe le cercle circonscrit en P. Le cercle de centre P passant par I coupe le cercle circonscrit en B et C !

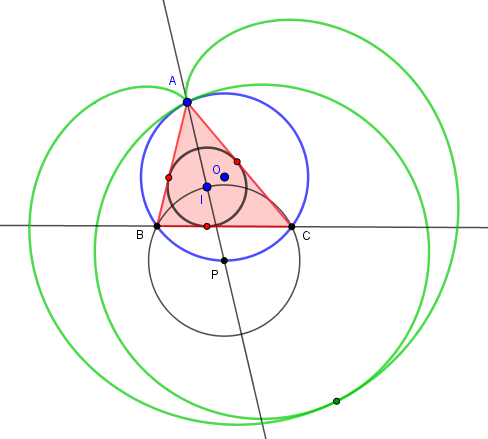
Si I est extérieur au cercle circonscrit, il ne peut plus être le centre du cercle inscrit, mais il peut être le centre d'un cercle exinscrit.
Si I est encore plus loin, ce n'est plus possible.
La limite est obtenue quand le cercle de centre P passant par I devient tangent au cercle circonscrit. Cette limite est une cardioide (exercice : le démontrer).
Avant celà, lorsque A devient intérieur au cercle (P,I), le cercle exinscrit ne l'est plus dans l'angle A, mais dans l'angle B ou C. Cette limite est un cercle homothétique de centre A et de rapport 2 du cercle circonscrit.