Triangles - Solutions

Construire un triangle ABC connaissant ...

Un sommet A, le centre du cercle inscrit I et le centre de gravité G

Le milieu M de BC est construit immédiatement avec GM = AG/2
Soient P et Q les points de contact des cercles inscrits et exinscrits avec la droite BC. MP = MQ     (PB = QC = p-b).
P' l'intersection de AQ avec le cercle inscrit est diamétralement opposé à P (homothétie de centre A). Ou encore I milieu de PP' et M milieu de PQ et par conséquent MI // QP' = AQ
Soit A' le symétrique de A par rapport à M. M milieu de AA' et M milieu de PQ donne A'P // AQ // MI.
D'autre part IP _|_ MP (=BC) et P est donc sur le cercle de diamètre MI.

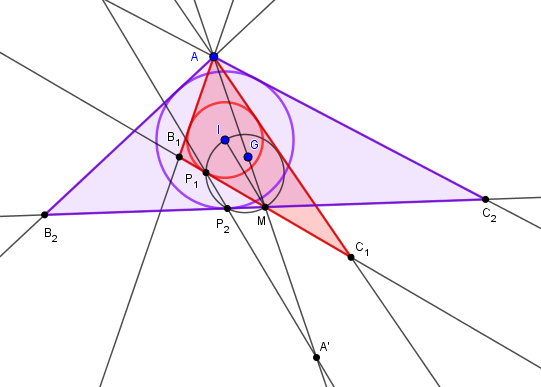Et finalement la construction :
Construire M avec GM=AG/2 puis A' avec MA'=MA
La parallèle à MI issue de A' coupe le cercle de diamètre MI en P
IP est alors le rayon du cercle inscrit, MP est la droite BC, les droites AB et AC sont les tangentes issues de A au cercle inscrit.
Nota : Selon la position de A,G,I, la solution obtenue peut être I centre d'un cercle exinscrit
(échange des rôles de P et Q). Enfin il peut y avoir 0, 1 ou 2 solutions.