Triangles - Solutions
Construire un triangle ABC connaissant ...
Un sommet A, le centre du cercle inscrit I et l'orthocentre H
Citation :
Suppose we put the incenter I at the
origin, A = (a, b) and H = (a, c) for b>0. Let r be the inradius of the triangle.
A fairly straightforward calculation gives :
(5) r² - r(b-c)/2 - (a²+bc)/2 = 0
If M is the midpoint of IA and P the orthogonal projection of H on the line
IA, then (a²+bc)/2 being the dot product of IM and IH, is the (signed) product
IM·IP.
Note that if angle AIH does not exceed a right angle, equation (5) admits
a unique positive root.
In the construction below we assume H closer than A to the
perpendicular to AH through I.
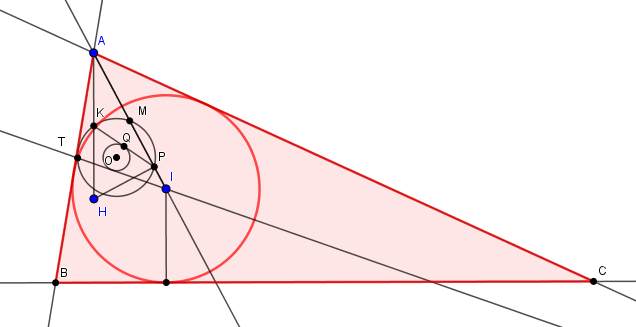 Given triangle AIH in which the angle AIH does not exceed
a right angle, let M be the midpoint of IA, K the midpoint of AH, and P the
orthogonal projection of H on the line IA.
Given triangle AIH in which the angle AIH does not exceed
a right angle, let M be the midpoint of IA, K the midpoint of AH, and P the
orthogonal projection of H on the line IA.
(1) Construct the circle (C) through P, M and K. Let O be the center of (C) and Q
the midpoint of PK.
(2) Construct a tangent from I to the circle O(Q) intersecting (C) at T, with T
farther from I than the point of tangency.
The circle I(T) is the incircle of the required triangle, which can be completed
by constructing the tangents from A to I(T), and the tangent perpendicular to AH
through the "lowest" point of I(T).
If H is farther than A to the perpendicular from I to the line AH, the same construction applies, except that in (2) T is the intersection with (C) closer to I than the point of tangency.
© P. Yiu FG200512.pdf in Forum Geometricum










