L'échelle et le tonneau
Soit x = OA la distance du pied de l'échelle au mur, y = OB la hauteur, L = AB la longueur de l'échelle
et r le rayon du tonneau.
Pythagore a dit : x² + y² = L² qui peut s'écrire (x + y)² - 2.x.y = L², et en appelant S = x + y et P = x.y : S² - 2P = L²
Le tonneau est en fait le cercle inscrit dans le triangle OAB.
L'aire de ce triangle est alors (x + y + L).r/2, et c'est aussi x.y/2,
soit x.y = (x + y + L).r, ou encore P = (S + L).r
En éliminant P : S² - 2.S.r - L² - 2L.r = 0, qui peut s'écrire :
(S + L)(S - L - 2r) = 0
La solution S = -L ne convient évidemment pas (S > 0) et donc S = 2r + L,
et P = (S + L).r = 2r(r + L)
x et y sont donc solution de l'équation X² - S.X + P = 0 soit
| X² - (2r + L)X + 2r(r + L) = 0 |
Le discriminant est
Δ = (2r + L)² - 8r(r + L) = L² - 4r² - 4r.L
En appelant L/R = t, Δ > 0 ssi t² - 4t - 4 > 0.
C'est à dire si t > 2 + √8 = 4.8284...
| L'échelle doit avoir une longueur supérieure à 1 + √2 = 2.4142 fois le diamètre du tonneau. |
Avec L = 3 et 2r = 1 ceci est respecté, et l'équation donnant x et y est X² - 4X + 3.5 = 0 soit
| y = 2 + √0.5 = 2.707 m, et x = 2 - √0.5 = 1.293 m |
Il y a bien sûr une construction géométrique pour cette simple équation du second degré.
Mais... le problème revient à construire un triangle ABC étant donnés
l'angle A (ici 90°), le côté BC = a (ici L), et le rayon r du cercle inscrit.
Présenté ainsi, le problème admet aussi une construction toute différente !
Donnons tout d'abord la construction "synthétique" à partir de l'équation ci-dessus.
Construisons OR = r, OP = 2r et RQ = L sur le sol.
Dans l'applet ci-contre R et Q déplaçables définissent r et L.
Sur le mur traçons OH = r + L/2.
La médiatrice de PQ et l'horizontale en H se coupent en J
Le cercle de centre J passant par P (et Q) coupe le mur en B1 et B2
OB1 et OB2 sont les solutions de l'équation :
OB1 + OB2 = 2OH = 2r + L
OB1.OB2 = OP.OQ = 2r(r + L)
Cette construction est ici très simple car l'angle A est de 90°
Le cas général du triangle ABC d'angle A donné quelconque peut se résoudre de même :
a² = b² + c² - 2b.c.cos(A)
Et 2×Aire = b.c.sin(A) = (a + b + c)r
etc... comme ci-dessus.
Les termes en sin(A) et cos(A) ne sont toutefois pas très sympathiques...
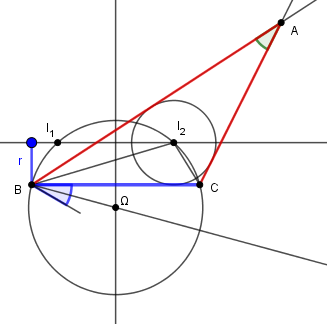Une construction générale d'un triangle ABC étant donnés A, a = BC et r est obtenue
à partir de la remarque suivante :
Soit I le centre du cercle inscrit, l'angle BIC = (A + π)/2
On construit ainsi facilement I, pour BC = a donné, comme intersection de
l'arc de cercle,
lieu des points I avec BIC = (A + π)/2, et de la droite à distance r de BC.
Puis on en déduit A.
Enoncés entiers
On veut donc L² - 4r² - 4r.L = m² carré parfait.Ceci s'écrit (L - 2r)² - 8r² = m² soit u² - 8r² = m² que l'on peut encore écrire (u + m)(u - m) = 8 r²
u + m et u - m étant de même parité, et donc tous deux pairs, u - m = 2k.q² et u + m = 4k.p²,
soit u = k.(2p² + q²) et m = k.(2p² - q²)
L'autre possibilité est u - m = 4k.p² et u + m = 2k.q², qui revient au même en valeur absolue.
On a donc au facteur k près :
| m = |2p² - q²|
r = p.q L = u + 2r = 2p² + q² + 2p.q |
Les solutions x et y sont donc L + 2r ± m soit x, y = (2p² + q² + 4p.q ± |2p² - q²|)/2 et donc :
| x, y = 2p² + 2p.q et q² + 2p.q |
Par exemple avec p = 2 et q = 1 :
r = 2, L = 13, x = 5, y = 12
p = 1 q = 1 donne
r = 1, L = 5, x = 3, y = 4, plus petites valeurs pour r et L,
mais l'échelle est très "couchée" (à 53° seulement)
