La géométrie du taxi - solutions
La distance n'est plus √x² + y² mais d = |x| + |y|.
 Taxi-droites
Taxi-droites
Combien y a-t-il de taxi-droites entre deux points A (0,0) et B (3,5) ?
Une taxi-droite entre le point (0,0) et le point (x,y) est formée de x segments horizontaux et y segments verticaux,
soit d = x+y segments en tout, plus courte distance entre A et B.
Il y a Cdx façons de choisir les x segments horizontaux parmi les d segments.
| N(x,y) = Cx+yx = Cx+yy = (x+y)!/(x! y!) |
N(3,5) = C83 = 8!/(3! 5!) = 56
 Balades
Balades
On veut aller d'un point A (0,0) au point B (1,2).
Le trajet le plus court (taxi-droite) a pour longueur x+y = 3.
Comme on l'a vu il y en a plusieurs et on les a même comptés.
Maintenant notre taxi en maraude veut aller de A à B en d > x+y segments unités.
Combien y a-t-il de trajets possibles ? (des allers retours sur un même segment sont autorisés) Le trajet va comporter, outre les segments normaux horizontaux (verts) et verticaux (rouges) :
- Des segments en marche arrière horizontaux (bleus)
- Des segments en marche arrière verticaux (mauves)
- Autant de segments verts et rouges supplémentaires pour compenser.
Soit q le nombre de segments verticaux en marche arrière (mauves).
Le nombre de segments en tout est :
x (segments normaux) + p (en marche arrière) + p (pour compenser) + y + q + q
Donc d = x + y + 2(p+q) = x + y + 2m
Et par conséquent : N(x, y, x+y+2m+1) = 0
Il y a donc x+p segments verts, p segments bleus, y+q segments rouges et q segments mauves.
Toute répartition de coloriages (R,V,B,M) sur les d segments respectant ces nombres de segments donne un chemin valide et réciproquement.
Il y a Cx+2p+y+2qx+p choix pour les x+p segments verts parmi d = x+2p+y+2q segments.
Restent p+y+2q segments pour lesquels Cp+y+2qp choix pour les p segments bleus.
Restent y+2q et Cy+2qy+q choix pour les y+q segments rouges. Le reste est les q segments mauves.
Donc au total : Cx+2p+y+2qx+p × Cp+y+2qp × Cy+2qy+q
et après simplification : d!/((x+p)! p! (y+q)! q!)
Reste maintenant à cumuler tous ces chemins pour toutes les répartitions de p+q = m, soit :
| N(x, y, x+y+2m) = Σp=0m (x+y+2m)!/((x+p)! p! (y+m-p)! (m-p)!) avec 0! = 1 |
N(1, 2, 5) = 5!/(1! 0! 3! 1!) + 5!/(2! 1! 2! 0!) = 50, (m = 1)
Trajets propres
Certains de ces trajets comportent des allers retours sur un même segment.Nous appellerons ces trajets des trajets impropres.
Les trajets propres ne comportant pas d'aller retours, mais pouvant toutefois comporter plusieurs passages (non consécutifs) sur un même segment.
Ce n'est pas une mince affaire de compter les P(x, y, d) trajets propres et les I(x, y, d) trajets impropres, d = x+y+2m.
On a bien entendu : N(x, y, d) = P(x, y, d) + I(x, y, d)
Soit un trajet propre de d segments.
A chacun des d+1 sommets traversés au cours de ce trajet, on peut ajouter un aller retour de 4 façons possibles.
Toutefois l'aller retour sur le segment ij est compté deux fois : une fois comme aller retour à partir de i, une fois à partir de j.
Il y a donc 4(d+1) - d = 3d+4 façons d'ajouter un aller retour à un trajet propre de longueur d.
I(x, y, d+2) = P(x, y, d)×(3d+4)
N(1,2,3) = 3, évidement propres, et donc I(1,2,5) = 3×(3×3+4) = 39
Sur les 50 trajets de (0,0) à (1,2) en 5 segments, il y a 39 trajets impropres et donc 11 trajets propres.
Par contre pour d > x+y+2 l'affaire se complique.
Trajets simples, trajets purs
 On définit des trajets "simples" qui ne passent jamais deux fois par le même segment.
Il sont donc propres.
On définit des trajets "simples" qui ne passent jamais deux fois par le même segment.
Il sont donc propres.
Cherchons à dériver des trajets à partir d'un trajet simple par "greffe".
Greffer un trajet de longueur 2 (un simple aller retour) sur un point du trajet a été vu ci-dessus.
Greffer un trajet de longueur impaire entre deux nœud du trajet simple conduit clairement à un segment répété (dans le même sens).
Ce n'est pas aussi simple pour un greffon de longueur paire > 2, car on peut ainsi obtenir un trajet simple plus long (avec croisement) ou un segment répété en sens inverse !
On est ainsi amené à considérer des trajets que nous qualifierons de "purs" :
qui ne passent qu'une seule fois par les nœuds visités.
Alors greffer un trajet de longueur quelconque entre deux nœuds (éventuellement confondus)
d'un trajet pur rend ce trajet "impur" :
on repasse obligatoirement deux fois aux nœuds de la greffe.
Il reste à compter le nombre de façons de greffer,
mais nous n'essaierons même pas...
Donnons juste un exemple encore raisonnable :
nombre de trajets de longueur 7 entre (0,0) et (1,2)
Le nombre total de trajets est 7!/(1!0!4!2!) + 7!/(2!1!3!1!) + 7!/(3!2!2!0!) = 735
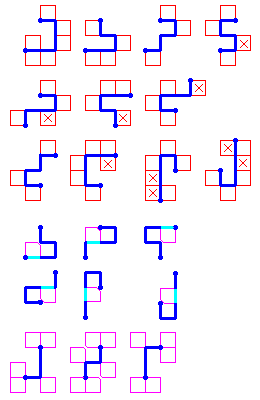
Les 11 trajets propres de longueur 5 (en bleu) vus précédement sont purs et simples.
On obtient les trajets purs de longueur 7 en remplaçant un segment d'un des trajets purs précédents
par un trajet (pur) de longueur 3 (en rouge) en faisant attention à ne pas reprendre un sommet déja visité.
On obtient ainsi 50 trajets purs de longueur 7.
Helas, on les obtient ainsi plusieurs fois et 9 d'entre eux (marqués d'un X) sont en double,
soit 41 trajets seulement.
On obtient des trajets simples en autorisant les passages multiples par le même nœud
et 6 trajets suplémentaires à partir des 11 trajets purs de longueur 5.
Mais ... il faut aussi considérer l'ajout d'une boucle de longueur 4 sur un nœud des trajets simples
de longueur 3, ce qui donne encore 16 trajets !
Mais ceux-ci incluent les 6 trouvés ci-dessus.
Quoi qu'il en soit, chaque boucle peut être parcourue dans les deux sens, et il faut doubler ce nombre.
On a ainsi 73 trajets simples de longueur 7, dont 32 impurs.
 Taxi-cercles
Taxi-cercles
On définit un "taxi-cercle" comme l'ensemble des points à taxi-distance R du centre O.
Un taxi-cercle est en fait un carré à 45 degrés !
Chaque côté comporte R intervalles, donc 4R points en tout sur la "circonférence"
La définition de taxi-π est ambigüe.
Si on la définit à partir du périmètre (éthymologiquement correct) :
Considérant que chaque segment à 45 degré a pour taxi-longueur 2, la taxi-longueur de cette circonférence est 8R donnant π = 4
Il nous faut maintenant définir la "taxi-aire" !
Si on la définit comme le nombre de carrés unité inclus dans le cercle,
l'aire du taxi-cercle est 2R², donnant π = 2
De toute façon la définition de la taxi-aire est douteuse ...
On ne peut la définir rigoureusement que pour des rectangles parallèles aux axes.
Dans le cas du cercle, on a même la propriété surprenante : on peut paver le plan avec des taxi-cercles !
Et quelle est la définition d'un rectangle non parallèle aux axes ??
(il y a plusieurs côtés possibles pour les mêmes sommets)
Finalement, il vaut mieux conserver :
| taxi-π = 4
Taxi-périmètre = 2πR |
 Taxi-ellipse
Taxi-ellipse
Ensemble des points dont la somme des taxi-distances aux foyers F et F' vaut d
Posons F (0,0) et F' (u,v). Soit M un point (x, v+a), 0 ≤ x ≤ u
La somme des taxi-distances de M à F et F' vaut FM + MF' = FF' + 2a = u + v + 2a = d.
La taxi-ellipse est inscrite dans le rectangle (-a, -a) (u+a, v+a)
u+v et d sont de même parité. Une taxi-ellipse avec FF' = 6 et d = 13 est impossible (ellipse imaginaire).
Le point N satisfait à FN + F'N = d = FF' + 2a si F'N = a, N est donc sur le quart de taxi-cercle de centre F' de rayon a.
La taxi-ellipse est donc composée de 4 segments verticaux et horizontaux et de 4 quarts de taxi-cercles.
 La hauteur des segment verticaux est nulle si les foyers ont même ordonnée.
La hauteur des segment verticaux est nulle si les foyers ont même ordonnée.
Foyers (-3,0) et (0,3) FF' = 6, d = 12 donc a = 3
 Taxi-ellipse imaginaire
Taxi-ellipse imaginaire
:
Lorsque FF' et d sont de parité opposée, il n'existe aucun point avec MF + MF' = d
Toutefois si on divise la grille par 2, FF' et d deviennent pairs et une ellipse existe sur ce nouveau quadrillage.
Tous les points de cette ellipse ont une coordonnée demi-entière.
Cette ellipse "imaginaire" sépare le réseau d'origine en deux régions :
- les points intérieurs avec MF + MF' < d
- les points extérieurs MF + MF' > d.
 Taxi-médiatrice
Taxi-médiatrice
Ensemble des points à égales taxi-distances de A et B.
NA = NH + HA, NB = NH + HB, si HA = HB tous les points N sur la verticale.
2 NA = 2 NB = AB + 2 NH. Donc AB doit être pair
MA = MI + IA = MB = MJ + JB = AB/2 pour tous les points M
 Si la taxi-distance AB est impaire, la médiatrice est "imaginaire" et ne comporte aucun point réel.
Si la taxi-distance AB est impaire, la médiatrice est "imaginaire" et ne comporte aucun point réel.
Par contre elle sépare bien le plan en deux régions MA < MB et MA > MB.
 La taxi-médiatrice donne lieu à une véritable horreur :
si x = y les points tels que P sont tous "sur" la médiatrice qui se compose,
outre un segment de droite, de deux quarts de plans entiers !
La taxi-médiatrice donne lieu à une véritable horreur :
si x = y les points tels que P sont tous "sur" la médiatrice qui se compose,
outre un segment de droite, de deux quarts de plans entiers !
Distances fractionnaires
Nous avons vu des cas où les points du réseau ne suffisaient pas (ellipse, droites imaginaires). En subdivisant le quadrillage, et par passage à la limite, on peut définir la taxi-distance de points quelconques. Les notions de points imaginaires précédentes disparaissent alors, et les courbes deviennent continues, mais gardent leurs angles : elles sont composées de segments de droite !Noter que compter les chemins de distances d entre deux points n'a alors aucun sens : il y en a une infinité.
Nous allons nous placer dorénavant dans ce cas, indispensable pour définir la
 Taxi-distance d'un point à une droite
Taxi-distance d'un point à une droite
On définit la taxi-distance d'un point à une droite comme la plus petite taxi-distance entre ce point et les points de la droite.
Il s'agit donc de la distance au point le plus proche horizontalement ou verticalement.
 Taxi-parabole
Taxi-parabole
Ensemble des points à égale taxi-distance du foyer F et d'une droite D.
FM la plus courte taxi-distance entre F et (D), S milieu de FM, FS = SM.
Les droites à 45 degrés issues de F coupent (D) en I et J. Les horizontales (resp. verticales) en I et J coupent la verticale (resp. horizontale) de F en A et B.
FA = AI et FB = BJ, les points A, B, S sont donc des points de la taxi-parabole.
Celle ci est alors composée de portions de droites et a une branche infinie horizontale (resp. verticale, selon la pente de (D) ).
 Si (D) est à 45 degrés, on obtient une "parabole équilatère" !
Si (D) est à 45 degrés, on obtient une "parabole équilatère" !
 Taxi-hyperbole
Taxi-hyperbole
Ensemble des points dont la différence des taxi-distances aux foyers F(0,0) et F'(a,b) vaut d.
Nous supposerons sans perte de généralité a ≥ b
Soit I tel que FI = d avec d < a-b. Alors tous les points de la taxi-médiatrice de F'I sont des points de la taxi-hyperbole. Les asymptotes sont verticales.
 Si d = a - b, la médiatrice comporte des quarts de plans, et l'hyperbole aussi.
Si d = a - b, la médiatrice comporte des quarts de plans, et l'hyperbole aussi.
 si a-b < d < a + b l'hyperbole à une asymptote horizontale et une verticale.
si a-b < d < a + b l'hyperbole à une asymptote horizontale et une verticale.
 Si d = a + b = FF' l'hyperbole dégénère en deux quarts de plans.
Si d = a + b = FF' l'hyperbole dégénère en deux quarts de plans.
Enfin si d > FF' l'hyperbole n'existe pas.
Si les foyers ont même abcisse ou même ordonnée, la taxi-hyperbole dégénère en deux droites.










