Bicolore
On dispose de papier bicolore, ici une face cyan une face rouge.Carré de papier → carré
Avec un carré de papier bicolore obtenir par pliage, sans aucune découpe, un carré bariolé.Dans les figures suivantes, les plis bleus sont vers l'avant (plis "vallée"), les plis magenta vers l'arrière (plis "montagne")
- - 2 plis suffisent, côté obtenu = 2/3
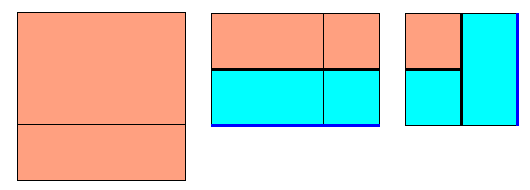
Pour obtenir une zone cyan d'un seul tenant il faut un pli de plus. 3 plis, côté = 2/3 :
- - 3 plis et côté = 1/2
- - 3 plis et côté = 2/3
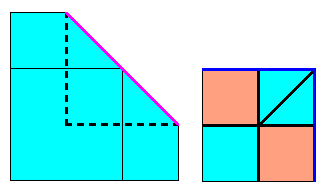
Pour obtenir une zone cyan d'un seul tenant, il faut 6 plis, côté obtenu = 1/2 :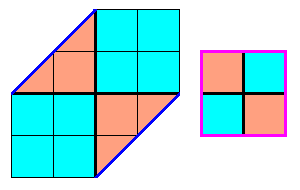
- - 4 plis et côté = 2/3
La zone cyan d'un seul tenant est obtenue avec 8 plis, côté = 1/2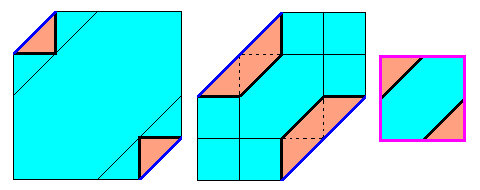
- - 4 plis, côté = √2/3
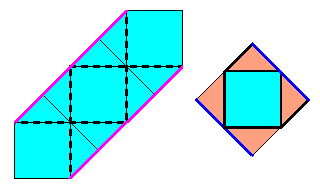
- - 4 plis, côté = 2/3
Bande de papier → cube
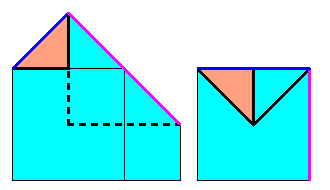
Envelopper un cube avec une bande de papier.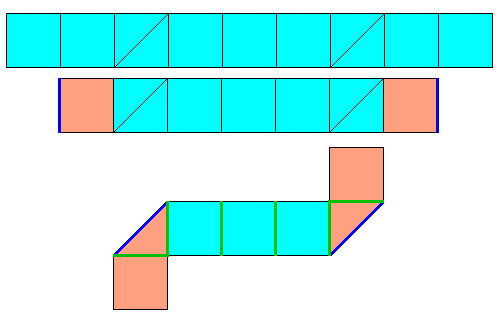
Au final la face arrière est entièrement rouge. En pliant (vers l'avant) tous les plis verts à angle droit, on forme un cube rouge.
Une des faces est formée de deux triangles accolés.
On obtient ainsi un patron du cube, formé de 5 carrés et 2 triangles au lieu du patron classique formé de 6 carrés.
Carré de papier → cube
A partir d'un carré de papier bicolore, tracer quelques coups de cutter en laissant le carré d'un seul tenant, puis plier pour recouvrir un cube d'aspect unicolore
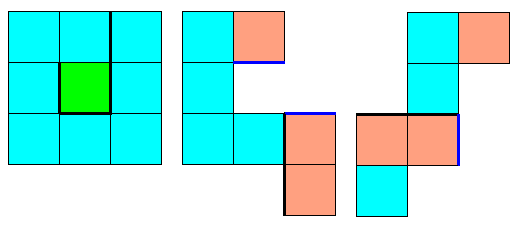
Il y a plusieurs solutions. Un des 9 petits carrés du quadrillage est "inutile", ici en vert. On peut aussi bien le découper et le jeter.
Pour respecter l'énoncé, on le rabat à plat à l'intérieur.
A symétrie près il y a trois façons de choisir ce carré vert, et les 3 solutions de base.
A noter que la découpe qui permet de rabattre ce carré vert peut varier, et de plus une fois cette découpe effectuée, cela laisse le choix du carré qui est "vert".
donnant lieu à diverses variantes.
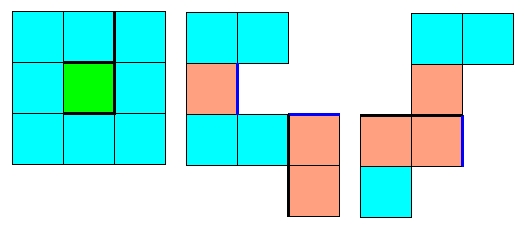
Dans chaque cas, on obtient un patron du cube où la face arrière est entièerement rouge.
On le replie en forme de cube par 5 plis vallées à angle droit.
- Carré vert dans un angle
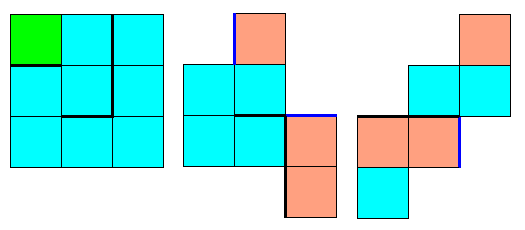
- Carré vert sur un côté
- carré vert au centre
Annexe : Bande de papier → tétraèdre etc...
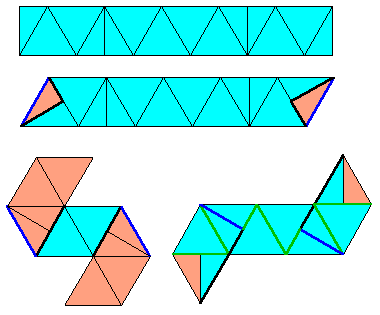
Il s'agit de trouver un patron du solide le plus "rectiligne" possible, et de parcourir ce patron.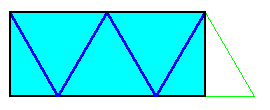
Pour le tétraèdre, c'est assez évident, et la couleur est traitée sans action suplémentaire, puisque le patron est
déja tout droit.
Là aussi, le patron "classique" formé de 4 triangles équilatéraux voit l'un d'entre eux remplacé par deux moitiés.
Si a est l'arète du tétraèdre, la bande de papier est de dimensions 2a × a√3/2
En d'autres termes la longueur de la bande est 4/√3 ≈ 2.3094... × sa largeur.
Ce patron d'un tétraèdre à partir d'un rectangle est utilisé dans les sachets de tisane "Pyramid®" de la marque Lipton™.
L'octaèdre nécessite déja, comme le cube vu précédemment, des "repliages" pour avoir une seule
couleur visible.
Ici les deux extrémités n'étant pas sur la même face de l'octaèdre, les deux bouts qui dépassent du patron sont
"en trop", et peuvent être planqués sous le tapis (repliés sur l'envers du patron).
In fine, on obtient un patron de l'octaèdre où la face arrière est entièrement rouge.
On termine de replier ce patron par les 7 plis vallées verts.
On voit apparaître le principe général des changements de direction de la bande au cours du parcours des faces successives, principe qui était déja à l'œuvre dans le cube.
La difficulté avec le dodécaèdre est essentiellement que chaque face nécessite au moins deux
passages (ou un repli).
A côté l'icosaèdre, même s'il a 20 faces, semble plus simple.
Devant la profusion de patrons possibles et le labyrinthe des parcours des faces sur ces patrons, on est heureusement
guidé par un fil d'Ariane : le circuit Hamiltonien unique sur le dodécaèdre,
représenté ici (en rouge) sur le graphe.
Ce circuit découpe le dodécaèdre en deux demi-patrons formés de 6 pentagones.
Mis bout à bout ils forment un circuit Hamiltonien sur le graphe dual où les sommets sont les faces du dodécaèdre,
Ce graphe dual est le graphe de l'icosaèdre !
Et vice versa, le graphe dual de l'icosaèdre (sommets représentant les faces de l'icosaèdre) est .. un dodécaèdre.
On dispose donc de circuits Hamiltoniens permettant d'avoir une chaîne de faces successives pour le parcours de
notre bande de papier, aussi bien sur le dodécaèdre que sur l'icosaèdre.
A noter que l'unicité du circuit Hamiltonien sur le dodécaèdre, à symétries près, implique l'unicité sur l'icosaèdre.
Traduit sous forme de patrons, cela donne un patron "linéaire" pour le dodécaèdre.
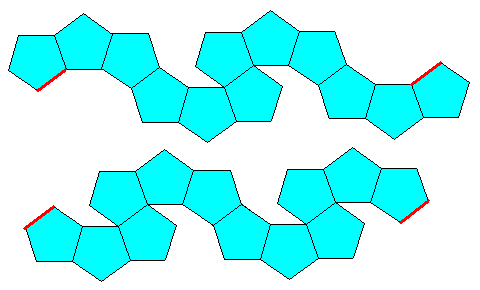
A noter aussi que le circuit étant fermé, on peut ouvrir la boucle en un point différent, ce qui ne change pas
grand chose en ce qui concerne le problème.
A voir plus tard si les virages "en épingle à cheveux" sont utiles ou nuisibles...
Les arètes soulignées sont en contact.
Et de même un circuit Hamiltonien des faces de l'icosaèdre :
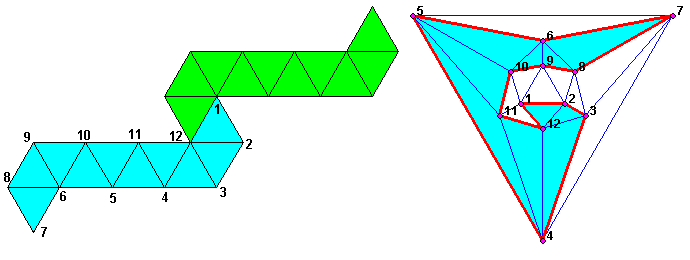
Les numéros des sommets correspondent aux faces du dodécaèdre ci-dessus.
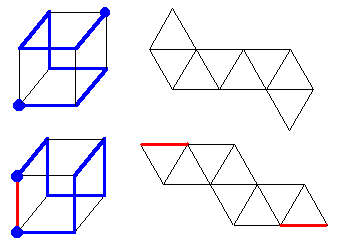Par contre il peut exister des parcours Hamiltoniens (non fermés) qui pourraient conduire à une solution.
Si on reprend le cas de l'octaèdre, le graphe dual est un cube, et il y a des parcours Hamiltoniens non fermés,
comme dans la première solution. La nouvelle solution obtenue avec un circuit fermé n'est pas plus courte.
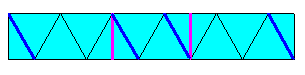
Les plis indiqués sont ceux pour obtenir le patron.
Revenons aux parcours des faces de l'icosaèdre (parcours Hamiltonien sur le dodécaèdre) et des faces du dodécaèdre (parcours Hamiltonien sur l'icosaèdre), en nous contentant de ces parcours qui sont en fait des circuits, sans chercher d'autres parcours non fermés.
Pour parcourir le patron de l'icosaèdre, on utilise la même technique que pour l'octaèdre pour effectuer les
changements de directions de la bande de papier, sans changer de couleur.
Les plis aux extrémités sont les mêmes que pour l'octaèdre.
Seuls les plis centraux sont détaillés ici.
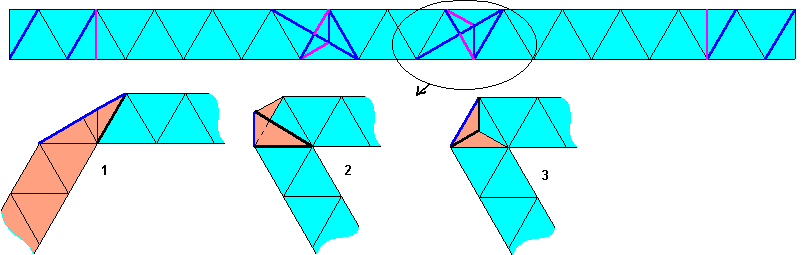
A la fin on obtient le patron de l'icosaèdre, la face arrière étant entièrement rouge.
On termine donc par les 19 plis vallée qui restent pour former l'icosaèdre.
Pour le patron du dodécaèdre, on ne cherchera pas ici les solutions où on revient sur une face ultérieurement,
pour "boucher les trous", et on cherche ainsi un pliage qui recouvre entièrement une face (un pentagone),
un côté étant unicolore. Contrairement aux pliages précédents du cube, octaèdre et icosaèdre, ici c'est la
face supérieure qui est unicolore, la face arrière étant bariolée. Mais si on y tient vraiment, on peut toujours
retourner les plis ...
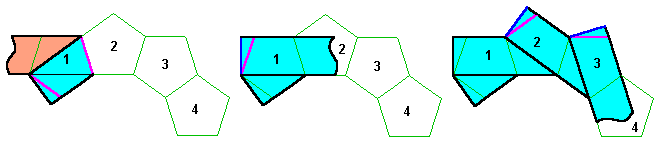
Attention au sens des plis. Le premier pli fait passer la suite de la bande par derrière, le deuxième pli
ramène la bande par devant en la repliant sur elle même.
Les petits bouts qui dépassent sont soit planqués par dessous, soit laissés pour être recouverts ultérieurement
par la face d'à côté, soit même, en retournant les plis, cachés dans le pli même.
Ils peuvent aussi être repliés par devant puisque l'arrière de ces petits bouts est bleu !
Mais c'est moins joli.
Sauf pour le premier triangle de début de bande qui doit être plié sous la face 1, ou laissé tel quel pour
pliage à plat ultérieur sur la face voisine (face arrière rouge !).
Le pliage se poursuit de la même façon sur la face suivante.
Les trois premières faces sont ainsi entièrement recouvertes de papier bleu.
Il s'agit maintenant de tourner dans l'autre sens pour poursuivre avec les faces suivantes :
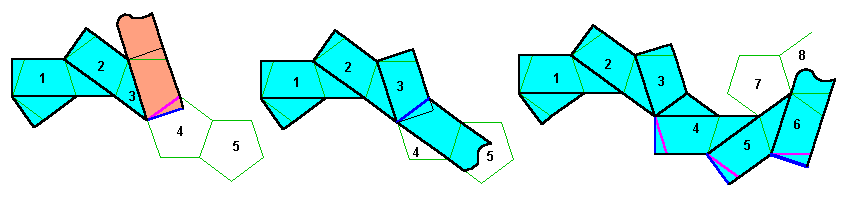
On poursuit alors les faces 4,5,6 comme pour les 3 premières.
Il faut maintenant effectuer le virage en épingle à cheveux précité.
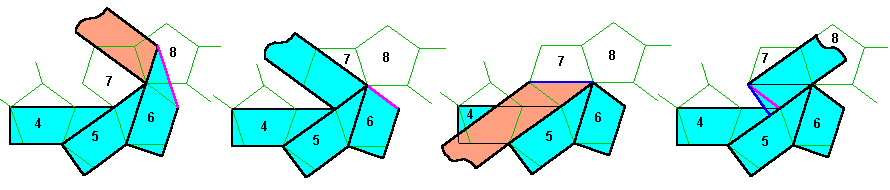
Là aussi attention au sens des plis sinon des morceaux rouges restent visibles !
Le petit bout qui dépasse de la face 7 est à planquer soit sous la face 7, soit sous la face 5 dans le dodécaèdre replié.
Une fois ce virage effectué, on se retrouve avec une bande qui démarre sur la face 7 exactement comme au début
sur la face 1.
On continue donc les faces 7..12 comme les 6 premières faces.
La réalisation pratique du pliage peut se faire "à plat" comme sur le patron décrit ci-dessus, il faut alors
terminer par les 11 plis montagne qui enroulent ce patron sur le dodécaèdre.
On peut aussi réaliser directement le pliage au fur et à mesure sur un dodécaèdre.
Dans les deux cas si on ne veut pas avoir un tas de papier en vrac au bout de quelques plis,
on peut coller au fur et à mesure.
La bande entière avec ses plis (les parties grisées sont cachées dans les plis) :
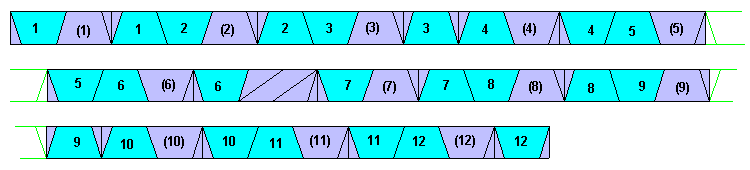
a étant l'arète du dodécaèdre, le largeur de la bande est a.cos(π/10) = a √10 + 2√5 / 4
et sa longueur 38a + 52a.cos(2π/5) = (25 + 13√5)a
Soit en prenant la largeur de la bande comme unité, une longueur de
(38 + 52cos(2π/5))/cos(π/10) = (100 + 52√5) / √10 + 2√5 = 56.851
En d'autres termes, un dodécaèdre d'arète 5cm nécessite une bande de largeur
5√10 + 2√5 / 4 = 4.75 cm et de longueur
5×(25 + 13√5) = 2.70 m !
Il est imaginable qu'il y ait plus court, puisque la partie cachée représente environ le tiers de cette longueur...
Mais il faudrait alors chercher à complèter les faces lors de passages ultérieurs et non de suite par un pli "aller-retour".
Votre challenge donc... en laissant tomber le fil d'Ariane des circuits Hamiltoniens.
