Le loup et l'agneau

Chacun son tour, le loup puis le mouton avance d'au plus un mètre.
La condition "au plus d'un mètre" est bien entendu là pour autoriser le loup à manger le mouton si celui-ci se trouve, au moment où c'est au loup de "jouer", à moins d'un mètre ! (sinon le loup serait obligé de dépasser le mouton sans le manger).

La stratégie "naïve" du loup qui fonce droit vers le mouton n'est pas efficace. Encore faut-il le prouver...
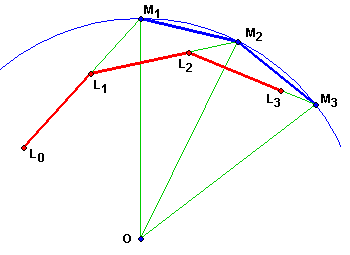C'est à dire que la distance L_iM_i reste strictement > 0, le mouton ayant été finallement acculé à tourner autour de l'enclos.
L_iM_i ≤ 0 implique que le triangle L_i-1M_i-1M_i-1 a son angle L_i-1M_i-1M_i-1 ≤ M_i-1L_i-1M_i-1
Or lorsque le mouton tourne autour de l'enclos, poursuivi par le loup, cet angle L_i-1M_i-1M_i-1 ne fait qu'augmenter, à mesure que le loup se rapproche du bord !

Le loup ne peut manger le mouton avec cette stratégie que si celui-ci est suffisamment près quand le mouton commence à tourner.

Il est nécessaire que le loup prenne de l'avance, en visant "devant" le mouton par rapport à la stratégie précédente. Mais viser trop loin devant va inciter le mouton à faire demi-tour et le loup est marron !

On arrive ainsi à une stratégie où le loup ne devant pas être pénalisé si le mouton fait demi-tour, se trouve sur l'axe de symétrie de l'enclos : le rayon joignant le centre au mouton. Que le mouton parte à gauche ou à droite ne fait alors aucune différence.
Bien sûr, au départ le loup ne sachant pas encore où est le mouton (ils choisissent leur place initiale indépendamment), le seul moyen pour lui d'être sur ce rayon, quelle que soit la position du mouton, est de se placer initialement au centre !
Et donc la stratégie du loup :

Il se place au départ au centre. A chaque coup il rejoint le rayon joignant le centre à l'emplacement actuel du mouton.

Comme on va le voir, cette stratégie lui garantit la victoire, c'est à dire assure que la distance Loup-Mouton devient strictement < 1m quand c'est au loup de jouer.

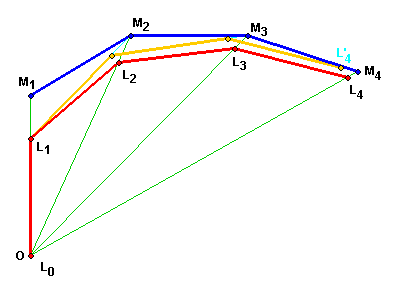Il est déja évident qu'il peut toujours jouer de cette façon, c'est à dire rejoindre ce fameux rayon : le triangle OM_i-1M_i ayant le côté M_i-1M_i ≤ a = 1m, on peut trouver un point L_i sur OM_i à distance a de L_i-1, tant que le loup est plus près du centre que le mouton.
La figure montre en orange le trajet qu'aurait suivi le loup avec son ancienne stratégie, il est visiblement plus proche maintenant du mouton qu'il ne l'aurait été.

Reste tout de même à prouver que ça suffit et qu'il va pouvoir manger.

Etudions déja ce qu'il advient du mouton s'il reste au bord.

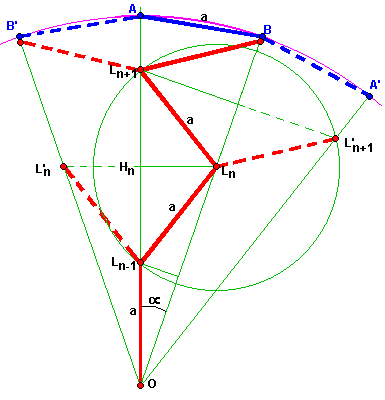
Par reflexion de la trajectoire autour du rayon, on peut replier la trajectoire dans un secteur, le mouton effectuant alors des aller-retours entre A et B.
Il revient au même que le mouton soit en B' et le loup allant alors en L'_n ou que le mouton soit en B et le loup aille en L_n, et de même pour chacun des coups.
On peut donc se limiter à étudier la trajectoire du loup confinée dans le secteur OAB, le mouton effectuant des aller-retours A↔B

On peut calculer les distances successives du loup au centre :
OH_n = (OL_n+1 + OL_n-1)/2 = OL_ncos(α) et sin(α/2) = a/(2R)
cos(α) = 1 - 2sin²(α/2) = 1 - a²/(2R²) donnent la relation de récurrence :

OLn+1 = 2(1 - a²/(2R²))OLn - OLn-1 OL0 = 0,    OL1 = a

Ce qui nous intéresse est de prouver que le loup atteint toujours la zone gagnante, à moins d'1 m du prochain coup du mouton. Une remarque géométrique va nous le permettre : L_n-1 et L_n+1 sont les intersections du cercle de centre L_n et de rayon a avec le rayon OA.

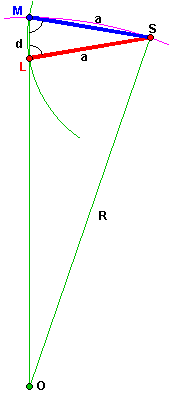Lorsque le loup est suffisamment proche de la cloture, son prochain coup le fait "sortir" de l'enclos, en d'autres termes le mouton est à moins de a du loup.
La valeur limite est d = a²/R, les triangles isocèles OMS et SML étant semblables ML/MS = MS/OM soit d/a = a/R.

Or comme tous les autres cercles de centre L_i sont plus proches du centre, les cordes L_i-1L_i+1 sont toutes ≥ d
Ceci garantit que le loup atteint la zone gagnante (L_i > R - d) en un nombre fini de coups.

Mais maintenant, ce mouton peureux dont la mort est assurée peut-il se transformer en mouton enragé, ne cédant pas un pouce de terrain devant le loup, et repoussant le moment où il sera acculé au bord de l'enclos ?
En d'autres termes il faut maintenant examiner ce qui se passe loin du bord, lorsque le mouton n'est pas autant limité dans ses déplacements.
Il est bien évident que même si le mouton refuse de reculer et reste à distance ≤ r du centre, le loup par la stratégie précédente va forcer le mouton à sortir du cercle de rayon r et le mouton n'aura fait que reculer l'échéance fatale.

En tout cas on peut considérer le disque de rayon a centré sur le mouton, ensemble des points accessibles au mouton, et le disque de rayon a centré sur le loup, ensemble des points accessibles au loup.
Le mouton doit bien entendu éviter le disque du loup !
Si le loup et le mouton sont suffisamment loin l'un de l'autre, il n'y a pas de problème. Si ces deux disques se recouvrent, cela limite les déplacements du mouton.

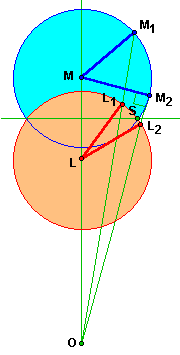Le mouton ne peut se placer que dans la zone bleue.
Le point de cette zone le plus proche du centre O est le "point de sureté" S, intersection des deux cercles et de la médiatrice de LM.
Si le mouton "fuit" le loup en M₁, le loup vient en L₁ sur le rayon OM₁ comme il se doit.
Le mouton peut aussi aller en M₂ dans le but de forcer le loup à s'éloigner le moins possible du centre en L₂.
Ce point "optimum" est celui qui rend l'angle MOM₂ le plus grand possible, c'est à dire que OM₂ est la tangente au cercle du mouton.
Enfin le mouton peut disputer le terrain au loup en allant au plus près du point S.
Cette dernière stratégie à pour but d'empêcher le loup de dépasser de beaucoup la perpendiculaire en L à OL.
Cela ne fonctionne bien sûr que si S est suffisamment proche de cette perpendiculaire, c'est à dire si le mouton est déja très près du loup ! La perpendiculaire en L à OL est alors à ε près MS = LS = la médiatrice de LM.
On est ainsi amené à la stratégie la plus efficace pour le mouton, empêchant au maximum le loup de s'écarter du centre :
Le mouton se place au début du jeu au plus près du centre, là où il pense que sera le loup, c'est à dire à a+ε du centre.
Il se place ensuite au plus près de S à chaque coup, forçant le loup à suivre une trajectoire à chaque coup pratiquement perpendiculaire au rayon.

A chaque coup on a la relation OL²_n+1 = OL²_n + a², soit OL_n = a√n

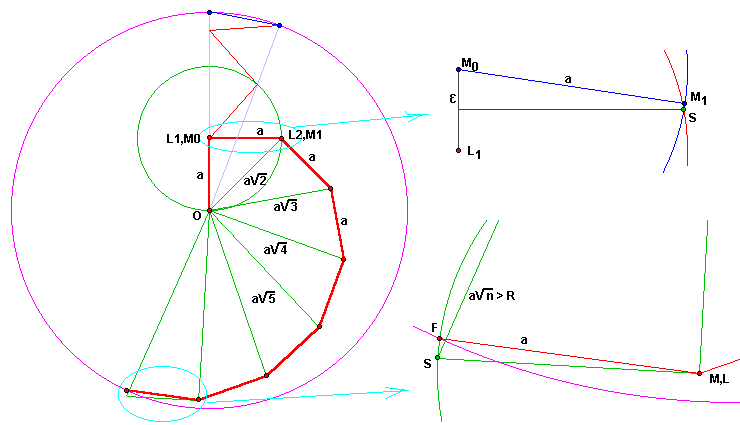
Au bout d'un temps fini on aura donc OL_n = a√n ≥ R, instant où le loup rattrappe le mouton au bord et le mange immédiatement.
On voit sur cet exemple l'efficacité de cette stratégie du mouton qui survit ici 8 coups au lieu de 4 s'il était resté au bord.
Toute autre stratégie pour le mouton laissera le loup s'approcher plus vite du bord, et donc manger le mouton plus tôt.

Si le point de départ du mouton est imposé, sa meilleure stratégie est de se rapprocher au plus vite du loup soit en se plaçant à chaque fois avec M_iM_i+1 perpendiculaire à OM_i+1, tant que ce point est > OS, et ensuite de se placer au plus près du loup (au plus près de S) pour forcer le loup à suivre une spirale en  a√n, soit en fonçant carrément droit sur le loup tant que c'est possible, puis par la même spirale que précédemment.

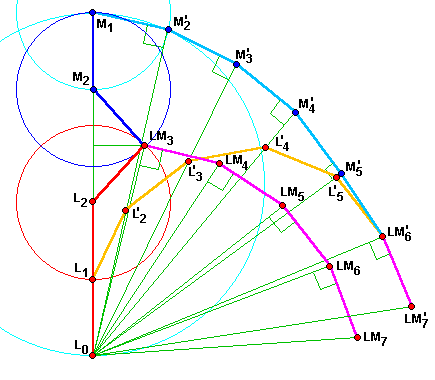Foncer droit vers le loup, s'avère finalement plus efficace qu'une fuite à 90°. Initialement le loup en L₀ et le mouton en M₁, le loup se dirige au premier coup droit vers le mouton, en L₁.
C'est maintenant au mouton de jouer en M₂, droit vers le loup, ou en M'₂ de sorte que le loup soit au moins loin possible du centre, en L'₂, au coup suivant.
Au coup suivant le mouton ne peut continuer l'attaque et il va en LM₃, rejoint de près par le loup, tout deux à ε du point de sécurité et entamant la spirale infernale LM₄, LM₅ etc...
Si le mouton poursuit sa stratégie "tangentielle" en M'₃, M'₄ etc... il doit l'abandonner en LM'₆ pour une spirale en  √n

Au final le loup et le mouton sont plus près du centre, assurant une survie plus longue du mouton, si le mouton a dès le départ foncé droit vers le loup !

Généralisation

Loin du bord, la stratégie est toujours valable et ne dépend pas en fait de l'enclos.
Le "centre" O peut donc être n'importe quel point sur la droite Loup-Mouton, le loup suivra au pire une spirale en  a√n, et s'éloignera de ce point plus vite si le mouton n'est pas aussi audacieux. Cette spirale rejoindra donc le bord en un temps fini (le loup mangeant le mouton en ce point) quel que soit la forme de l'enclos, le point de départ choisi et les mouvements du mouton.
C'est à dire au pire un n pour lequel OL_n ≥  a√n ≥ max(OP) pour tous les P du bord.

Un exemple de trajectoire dans un enclos de forme quelconque.

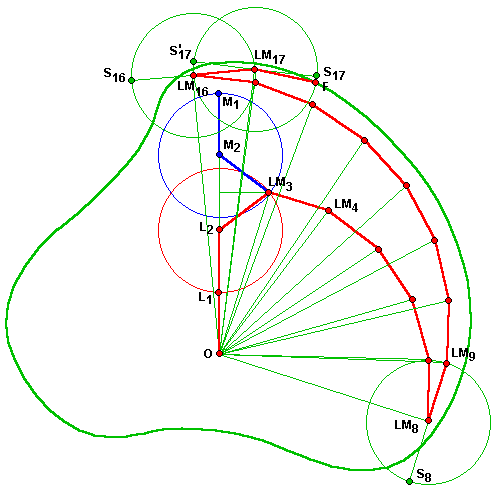
Ici le mouton commence par aller droit vers le loup au point M₂. Puis à ε du point de sécurité, presque rejoint par le loup en LM₃, tous deux entamant la spirale où les positions du mouton et du loup sont à ε près les mêmes. Cette spirale se poursuit jusqu'en LM₈.
Le point de sécurité S₈ en suivant la spirale est à l'extérieur de l'enclos et est donc mortel. Heureusement pour le mouton, la forme irrégulière de l'enclos et le centre quelconque lui permet de choisir le point de sécurité de l'autre côté ! Il fait donc demi-tour et va en M₉ suivi par le loup bien sûr, les deux étant toujours voisins de ε
Cette possibilité de demi-tour salvateur lui était refusée dans l'enclos circulaire, symétrique par rapport au rayon.
Il effectue un deuxième demi-tour semblable en M₁₆.
Hélas, arrivé en M₁₇ les deux points de sécurité sont tous deux en dehors de l'enclos et il se fait manger en F au coup suivant. Au mieux F étant une des intersections de la frontière avec le cercle de rayon a centré en M₁₇, point qui par la définition du point de sécurité est à moins de a du loup L₁₇!