Quadrilatères semblables
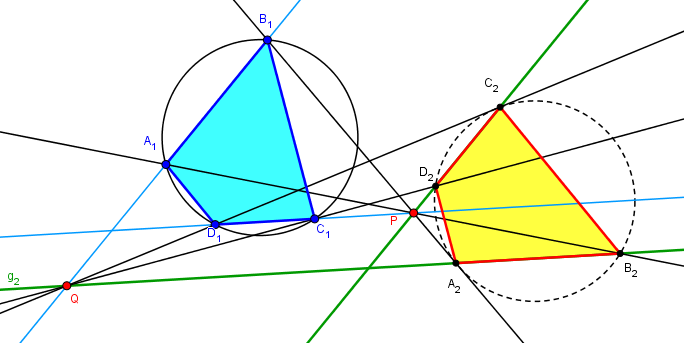
Source : Zwei Kreisvierecke sur de.sci.mathematikEtant donné un quadrilatère inscriptible A1B1C1D1.
Pour chaque point P sur la droite C1D1, et chaque point Q sur A1B1 :
Tracer la parallèle (g1) à A1B1 en P, et la parallèle (g2) à C1D1 en Q.
La droite PA1 coupe (g2) en B2, la droite PB1 coupe (g2) en A2
La droite QC1 coupe (g1) en D2, la droite QD1 coupe (g1) en C2
Propriété (à prouver) :
Le quadrilatère A2B2C2D2 est semblable au quadrilatère A1B1C1D1,
(donc est aussi inscriptible).
Les points A1,B1,C1,D1 peuvent être déplacés sur le cercle,
le quadrilatère n'a pas besoin d'être convexe.
P et Q peuvent être déplacés sur les droites (entières) C1D1 et A1B1
La propriété est généralement fausse si A1B1C1D1 n'est pas inscriptible.