Tangente commune

Construire les tangentes communes à un cercle et une parabole.
Cas où le cercle est centré sur l'axe de la parabole.

Soit AT une tangente commune, tangente en A au cercle de centre O.
Soit M la projection du foyer F sur cette tangente, donc sur la tangente au sommet à la parabole.
Considérons le point A' symmétrique de A par rapport à M et le cercle tangent en A' à AT, centré sur l'axe de la parabole en O'
Par projection perpendiculairement à AT, F est le milieu de OO' D'autre part la tangente au sommet, perpendiculaire à l'axe et passant par le milieu de la tangente commune AA' au deux cercles est donc l'axe radical de ces deux cercles.

Les tangentes communes à une parabole de foyer F et un cercle centré en O sur l'axe   sont tangentes à un deuxième cercle de centre O' symétrique de O par rapport au foyer F,   et ayant la tangente au sommet comme axe radical avec le cercle donné.

Dans l'applet, les points bleus F, S, O, r définisent la parabole et le cercle.

Ceci permet ainsi la construction cherchée :

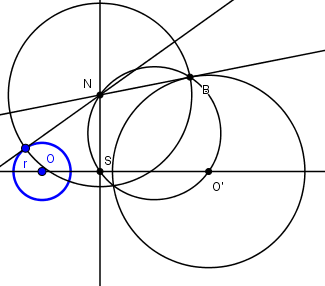
• Construire O' symétrique de O par rapport à F
• Une tangente quelconque (en r) à (C) coupe l'axe radical (la tangente au sommet) en N
• Le cercle de centre A passant par r et le cercle de diamètre O'N se coupent en B et le cercle cherché est le cercle de centre O' passant par B
  En effet la tangente en B à ce cercle est la droite BN et BN = rN, donc les puissances de N par rapport à ces deux cercles sont bien égales
  (Le cercle (N, Nr) est un cercle orthogonal aux deux autres, mais le choisir via la tangente en r est commode)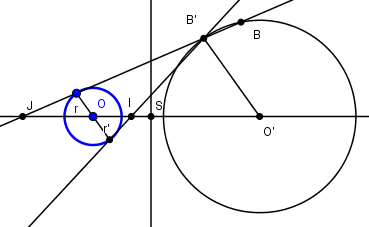
• B et r sont anti-homologues dans une similitude entre les deux cercles :
  le point B', homologue de r dans cette même similitude est la seconde intersection de rB avec le cercle
  et r', diamétralement opposé à r, est l'homologue de B' dans l'autre similitude
• Ceci donne les centres de similitudes et donc les tangentes communes, issues de ces centres I et J
• Le point de contact avec la parabole s'obtient à partir de l'intersection M de cette tangente avec la tangente au sommet,
  car il est sur la parallèle à l'axe en H, symetrique de S par rapport à M

Selon la position du cercle il y a 0, 2 ou 4 tangentes communes, éventuellement confondues par paires.

Si le cercle donné est centré en F, la construction échoue : les deux cercles (O) et (O') sont confondus.
Mais à la limite, le milieu de leur tangente commune est l'intersection du cercle donné avec l'axe radical,
La tangente commune est donc la tangente à (O) en l'intersection de ce cercle avec la tangente au sommet.
L'applet ne traite pas ce cas particulier.
Si (O) est tangent à la parabole, le cercle (O') devient un cercle point, l'applet ne traite pas ce cas non plus
(La tangente commune est la tangente issue de O')
Si (O) est tangent en S à la parabole, la tangente commune en S n'est pas non plus construite (à cause de la méthode employé ici pour construire les tangentes communes à deux cercles).

Si le cercle n'est pas centré sur l'axe, la construction à la règle et au compas n'est en général pas possible (équation générale de degré 4)