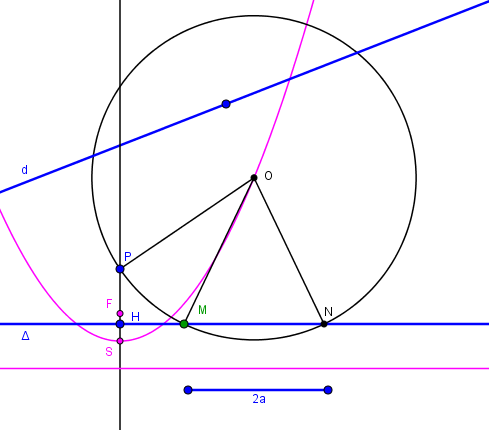
Cercle cherché

Construire un cercle centré sur une droite donnée (d) passant par un point donné P et coupant une droite donnée (Δ) en une corde de longueur donnée 2a.
Source : Geometriagon #1429

Considérons le lieu des centres des cercles passant par P et définisant une corde de longueur 2a sur (Δ).
Analytiquement, il n'est pas dificile de prouver qu'il s'agit d'une parabole dont nous allons expliciter les caractéristiques géométriques.
Soit O (x, y) le centre d'un tel cercle, et donc M = (x-a, 0) et N = (x+a, 0)
OP² = OM² s'écrit, avec P = (0, h), x² + (y - h)² = a² + y², ou encore :

  2hy = x² + h² - a² 

Le sommet S est évidemment défini par le centre du cercle circonscrit à PM_oN_o avec M_o,N_o = (±a, 0).
Analytiquement (X² = 2pY), le paramètre de cette parabole est h = PH, et donc le foyer F est à SF = HP/2 = h/2 et la directrice à distance PH = -h du foyer.

Dans l'applet, le point 2a définit la longueur de la corde, la droite (d) est définie par ses deux points bleus.
P est déplaçable sur la verticale en H (déplaçable aussi)
Le point M sur Δ, draggable, définit un cercle courant.

   

La construction cherchée est alors la construction classique des points d'intersection d'une droite (d) avec une parabole de foyer F et de directrice δ

La construction générale échoue si P est sur (Δ), mais alors la construction est évidente !
Si (d) est perpendiculaire à (Δ), c'est à dire parallèle à l'axe de la parabole, l'applet échoue.
Il n'y a alors qu'une seule solution, de construction évidente car (d) est la médiatrice de MN.