Ellipse inscrite d'excentricité donnée

Etant donné un rectangle de dimension 2a > 2b
Inscrire dans ce rectangle une ellipse d'excentricité donnée

En appelant u ≥ v les demi-axes de l'ellipse, la distance focale 2c est donnée par c² = u² - v² et l'excentricité par e = c/u soit e² = 1 - v²/u²
Se donner l'excentricité revient à se donner le rapport v/u

Théorème

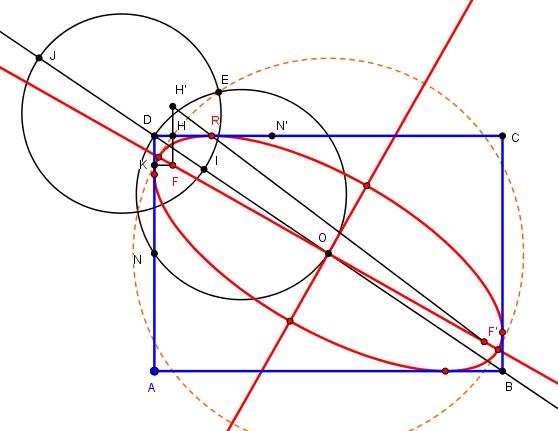
Le lieu des points d'où on peut tracer deux tangentes perpendiculaires à une ellipse est le cercle orthoptique ou cercle de Monge

On en déduit que toutes les ellipses inscrites dans un rectangle de dimension 2a > 2b, de demi-axes u > v sont caractérisées par

u² + v² = a² + b² = R² = cte où R est le rayon du cercle de Monge, circonscrit au rectangle ABCD

On obtient alors celle d'excentricité, ou de rapport v/u donné.
Soit I et J les points divisant OD dans le rapport v/u, c'est à dire ID/IO = JD/JO = v/u.
Le lieu des points E avec ED/EO = v/u est le cercle de diamètre I J
Le lieu des points avec EO² + ED² = NO² + ND² = a² + b² est le cercle de diamètre OD
On obtient ainsi le point E avec EO = u, le demi-grand axe de l'ellipse, et donc le cercle principal est le cercle de centre O de rayon OE
Ce cercle coupe les côtés (tangentes) en H et K qui sont les projections du foyer sur les tangentes, d'où F, puis F', les axes et les sommets.
Les points de contact s'obtiennent comme R = intersection de F'H' avec CD, H' étant le symétrique de F par rapport à CD.
Puis P,Q,S par QR // BD et symétrie par rapport à O.

Dans l'applet A définissent le rectangle ABCD, contraint à AB > BC > 0
Le point I définit u/v = IO/ID
A noter que I est restreint à une portion de OD, à la limite les axes de l'ellipse sont perpendiculaires au cotés
Au dela de cette droite l'ellipse n'existe pas (dans la construction le cercle principal ne coupe pas le côté AD)
Si I vient en D, l'ellipse dégénère en la diagonale BD, d'excentricité = 1. Le rapport v/u = 0

Angle des axes

On peut chercher l'angle des axes de l'ellipse d'excentricité e donnée dans un rectangle donné 2a > 2b
Considérons les projections des foyers sur la tangente CD, FH = x, F'H' = y

Théorème

Le produit des distances des foyers à une tangente est constant et égal au carré de demi petit axe xy = v²

D'autre part, x + y = 2b (O milieu de FF')
v est donné par u² + v² = a² + b² et v²/u² = 1 - e² et enfin la distance focale 2c obtenue par c = eu
On a donc tout ce qu'il faut pour calculer l'angle de FF' avec l'axe du rectangle par sin(α) = |x - y|/(2c)

u² = (a² + b²)/(2 - e²), et v² = (a² + b²)(1 - e²)/(2 - e²)
c² = e²u² = e²(a² + b²)/(2 - e²)
sin²α = ((x + y)² - 4xy)/(4c²) = (b² - v²)/c²

sin²α = ((b² - (1-e²)a²) / (e²b² + e²a²)

Avec v = 2u (e = √3/2), et a = 3b/2 (rectangle de 32×48)
sin²α = 7/39 soit α = 25°

Nota : Cette ellipse avec u = 2v est donc telle que le triangle formé par un foyer et les sommets est équilatéral, puisque c = 2v √3/2

Ellipse d'aire maximale

On a vu la relation u² + v² = a² + b² = cte pour toutes les ellipses inscrites.
Mais il faut remarquer que l'on a aussi les inégalités :

0 ≤ v ≤ b ≤ a ≤ u ≤ √a² + b²

(preuve : la distance du centre à une tangente d est v ≤ d ≤ u,
car tout point de l'ellipse est entre le cercle de rayon v et le cercle principal de rayon u)

L'aire = πuv est maximale ssi u²v² est maximale.
Avec les contraintes u² + v² = a² + b² et les inégalités ci dessus

Théorème

Le produit de deux nombres de somme constante est maximal quand ils sont égaux.

Ici le produit des deux nombres u² et v² de somme constante a² + b² est maximal quand u = v.
Comme v < b < a < u, le maximum de la fonction monotone croissante Aire S = f(v) avec v dans [0, b] est pour v = b
(le maximum de v par dS/dv = 0 serait au dela de cet intervalle)

L'ellipse inscrite d'aire maximale a pour axes les médianes du rectangle

C'est à dire que les points de contact sont aux milieux des côtés du rectangle.

 Etant donné un point de contact

 Etant donné les axes