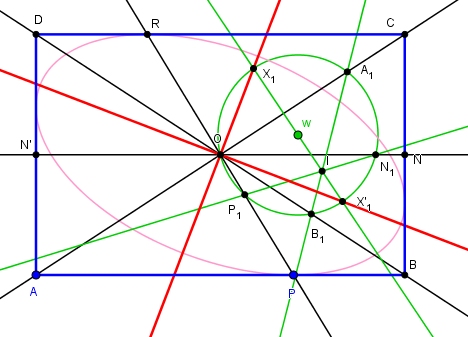
Ellipse inscrite

Etant donné un rectangle de dimension 2a > 2b (disons pour fixer les idées 32 cm sur 48cm)
On se propose d'étudier les ellipses inscrites dans ce rectangle, c'est à dire tangentes aux 4 côtés du rectangle.
Il en existe bien entendu une infinité.
On cherchera tout d'abord à construire celle ayant :

• le point de contact avec le grand côté donné
• ou bien direction des axes donnée
• ou bien excentricité donnée

On cherche aussi celle ayant la plus grande aire possible.

Tout d'abord la symétrie évidente de la figure implique que le centre de l'ellipse est le centre du rectangle.
Pour s'en convaincre formellement, il suffit de considérer les deux tangentes parallèles formées par deux côtés.
La droite joignant les points de contact est la polaire du point d'intersection (point à l'infini) des deux tangentes.
Le centre est le milieu de cette corde, sur la médiane relative aux deux autres côtés.
Et de même pour les deux autres côtés.
On rappellera aussi les propriétés connues de l'ellipse : foyers, cercle principal, cercle directeur, propriétés des tangentes..

Ellipse étant donné un point de contact

Il s'agit de déterminer les 3 autres, puis les foyers et les axes.
Considérant les deux tangentes issues de A, la droite PS reliant les points de contact a son milieu sur la diagonale OA.
Et de même en considérant les tangentes isues de B.
PQRS est donc un parallélogramme, à côtés parallèles aux diagonales de ABCD, d'où la construction immédiate de QRS étant donné P

Reste maintenant à construire les foyers et les axes.
On peut construire les axes en considérant les paires de diamètres conjugués suivantes :

• Les diagonales AC et BD
• une médiane NN' et la droite reliant les points de contacts "opposés" PR

On définit ainsi une involution du faisceau de droites O*
La paire de droites orthogonales qui se correspondent dans cette involution sont les axes de l'ellipse.
Construction classique en projettant cette involution de O* sur un cercle quelconque passant par O.

Les foyers sont obtenus comme conjugués harmoniques des intersections X et X' de la tangente et de la normale en P avec l'axe focal,
c'est à dire à partir de OF² = OF'² = OX.OX' (construction classique encore)

Le cercle principal est obtenu par la propriété classique que la projection H du foyer sur la tangente est sur ce cercle principal.
S'en déduisent immédiatement les sommets de l'ellipse, et son tracé par affinité du cercle principal dans le rapport OV/OU.

Dans l'applet A et B définissent le rectangle (parallélogramme) ABCD.
P définit le point de contact avec AB
Lors de la construction des axes, w choisit le "cercle quelconque passant par O".
La construction précédente de OF² = OF'² = OX.OX' échoue si l'axe focal est parallèle à AB, c'est à dire si P vient en M.
L'applet interdit ce cas en restreignant sans perte de généralité P au segment MB - ε.

Nota : La construction précédente ne fait pas intervenir les angles droits du rectangle ABCD, elle est donc valable sans aucun changement pour un parallélogramme ABCD.

 Etant donné la direction de l'axe

 Etant donné l'excentricité