2 cercles
Construire deux cercles égaux et mutuellement tangents, l'un tangent à deux côtés d'un rectangle, l'autre aux deux autres côtés.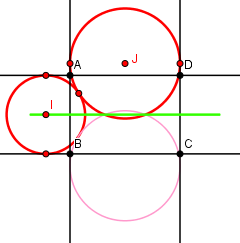
Les deux paires de droites formant un rectangle ABCD
Des cercles tangents à des côtés opposés ont l'un comme diamètre la largeur du rectangle, l'autre sa longueur et ne peuvent être égaux que si ce rectangle est un carré, il y a alors une infinité de solutions.
La suite considère donc des cercles chacun tangent à une paire de côtés adjacents !
Il y a plusieurs possibilités selon que les cercles sont intérieurs ou extérieurs au rectangle.
Aux symétries et permutations près, il y a 4 familles de cercles, selon les angles respectifs contenant chacun d'eux.
Sans perte de généralité, on peut considérer les angles opposés A et C.
Les deux angles extérieurs sont impossible (les cercles ne peuvent se toucher)
L'angle C est donc intérieur et les 4 possibilités pour le choix de l'angle A donnent les 4 familles.
Les permutations de ABCD et les symétries multiplient en fait les familles de sorte que au
total il y a xx paires de cercles solution.
Le problème est de construire ces cercles, pour chacune des familles.
Une figure montrant un représentant de chacune de ces familles.
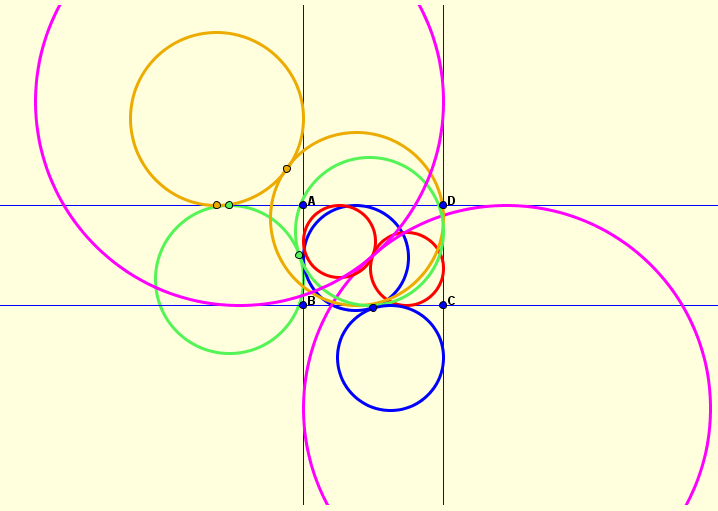
Les autres cercles d'une même famille ne sont pas montrés, mais s'obtiennent par symétries (au sens large)
et sont donc composés de cercles tous égaux à ce représentant.
On remarque que la première famille a en fait deux représentants possibles différents : rouge et magenta.
Les cercles rouges étant le seul cas où les cercles sont intérieurs au rectangle, si le format de ce rectangle est
1/2 ≤ BC/AC ≤ 2
Constructions
A vous de jouer...
