2 cercles

Construire deux cercles égaux et mutuellement tangents, l'un tangent à deux côtés d'un rectangle, l'autre aux deux autres côtés.

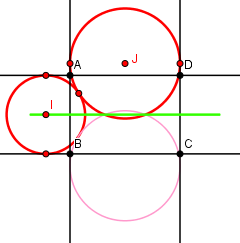
Deux côtés opposés

Les cercles ne peuvent être égaux que si le rectangle est en fait un carré
Quoi qu'il en soit, il y a une infinité de solutions.
Les cercles sont bien entendus centrés sur les médiatrices de AB et BC
Choisissons un point I arbitraire de la médiatrice de AB
La distance des centres est égal à (AB + BC)/2, somme des deux rayons.
Le centre J est donc l'intersection de la médiatrice de BC et du cercle de centre I et de rayon (AB + BC)/2
La construction est possible seulement si I est sur le segment de longueur AB + BC centré sur le centre O du rectangle.

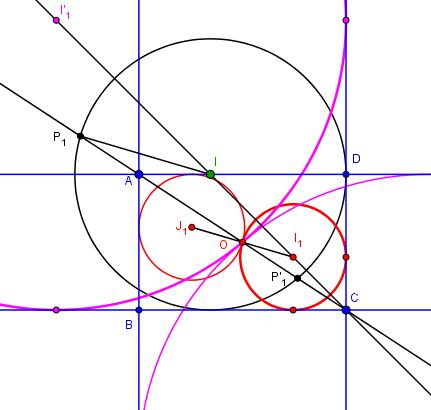
Deux côtés adjacents cas 1 et 1b

Les deux cercles s'échangent par une symétrice centrale de centre O, et leur point de contact est donc ce centre O
Le problème revient alors à construire un cercle tangent à BC et CD et passant par O, construction classique s'il en est :
Une homothétie de centre C laisse inchangée la droite CO, d'où la construction.
Tracer un cercle quelconque tangent à BC et CD, centré sur la bisectrice de l'angle C donc.
La droite CO coupe ce cercle en P1 et P2, homothétiques de O et donc le cercle cherché est l'image du cercle quelconque dans l'homothétie de rapport CO/CP
Les deux points P conduisent aux deux solutions rouge et magenta.

(L'applet est commune à tous les cas)

Dans l'applet, le rectangle est défini par les sommets déplaçables A et C.
Le cercle quelconque est centré à l'intersection i de la bissectrice et de la droite AD, ce qui permet d'obtenir instantanément son point de contact D avec CD.
Les points de contact du cercle (I) avec CD et BC sont alors obtenu par l'homothétie, puis la symétrie par rapport à la bissectrice.
Le deuxième cercle de la paire est obtenu par la symétrie centrale de centre O (homothétie de rapport -1 en fait).
L'homothétie est obtenue directement, et non pas en traçant la parallèle OI à Pi (qui échouerait si ABCD était un carré)
L'applet rate si le rectangle ABCD est en sens inverse (échange des bissectrices intérieures et extérieures de l'angle C)

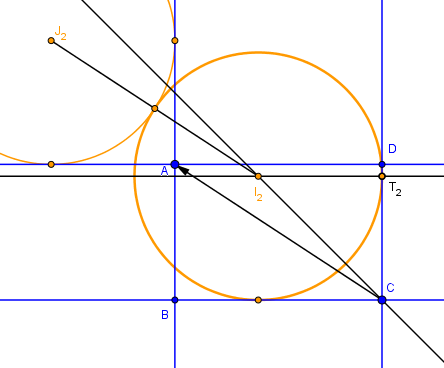
Deux côtés adjacents cas 2

Les deux cercles et surtout les angles qui les "contiennent" se déduisent l'un de l'autre par une translation de vecteur AC.
La distance des centres est donc AC et ceci donne la valeur de leur rayon AC/2.
La construction d'un cercle de ce rayon et centré sur la bissectrice de l'angle C n'est alors qu'une formalité :
Le point de contact T s'obtient avec CT = CO = AC/2. Le centre I est l'intersection de la bissectrice de l'angle C avec la parallèle à BC en T. L'autre point de contact est le symétrique par rapport à la bissectrice.
Le deuxième cercle de la paire et ses points de contacts se déduisent du premier par translation de vecteur CA.
Le point de contact des deux cercles est bien entendu le milieu de IJ.

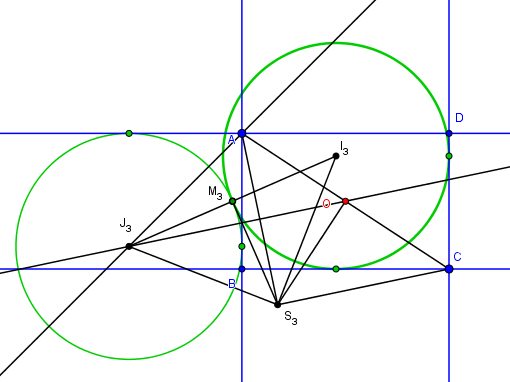
Deux côtés adjacents cas 3

Les deux cercles et surtout les angles qui les "contiennent" se déduisent l'un de l'autre par une rotation de 90° transformant A en C et la droite AB en la droite CB.
Le centre de cette rotation S est donc construit sur la médiatrice de AC, avec OS = OA = OC, le triangle ASC est isocèle rectangle.
Soit M le point de contact des deux cercles. Le triangle ISJ est aussi isocèle rectangle et aussi le triangle JMS
Soit T le point de contact du cercle avec AD le triangle JTA est isocèle rectangle
Bien sûr JM = JT = rayon, ces deux triangles JMS et JTA sont donc égaux et JS = JA
J est donc sur la médiatrice de SA, et c'est l'intersection de cette médiatrice avec la bisectrice de l'angle A (extérieure).
I s'en déduit par la rotation de centre S de 90°, et M milieu de IJ donne les cercles.

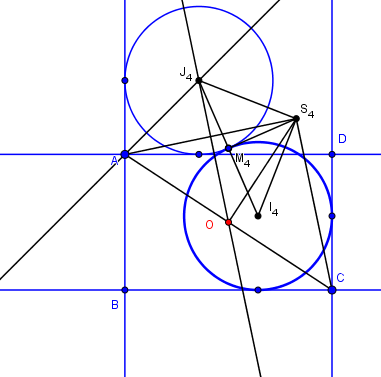
Deux côtés adjacents cas 4

Idem, simplement la rotation est de sens opposé : le point S est de l'autre côté de AC et il suffit juste de changer le signe de la rotation dans l'applet !