La règle seule
Les constructions présentées ici se font avec une règle à un seul côté, non marquée. C'est à dire que l'on peut :• tracer une droite passant par deux points connus
• Obtenir de nouveaux points par intersections de droites ainsi tracées
ou avec une courbe (eg. cercle) préalablement tracée par ailleurs (= donnée).
• Choisir un point arbitraire, si la construction finale ne dépend pas de ce choix.
Et c'est tout. Toute autre opération est illégale.
Enfin on se place dans un plan "ordonné" c'est à dire que l'on peut déterminer sur une droite
si deux points sont du même côté ou non d'un troisième.
Cette dernière précision est indispensable ici, car les constructions à la règle seule
ont pour cadre "naturel" le plan projectif dans lequel cette distinction n'a pas lieu entre ABC et ACB.
Les transformations du plan mises en jeu sont les "colinéations", c'est à dire les homographies générales.
Il n'y a alors pas de conservation des rapports de distance, seuls les birapports sont conservés.
La notion de milieu n'existe donc pas.
Quant à la notion de parallèle, elle est transformée en notion de points à l'infini.
Tracer une parallèle à une droite donnée revient à tracer une droite passant par l'intersection de cette droite
avec la droite de l'infini.
Celle-ci doit donc être donnée (par deux de ces points), ou le point à l'infini donné (par deux parallèles données)
Tracer une parallèle à une droite donnée seule est impossible.
Conjugué harmonique
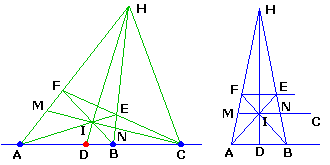Etant donné trois points alignés A,B,C, construire le conjugué harmonique de C
(c'est à dire DA/DB = -CA/CB).
On utilise ici une propriété projective du quadrilatère complet :
| Soit I l'intersection des diagonales AE et BF, M et N les intersections de DI avec les côtés, (C,I,M,N) est une division harmonique. |
L'application de Thalès suffit alors à prouver que I est le milieu de MN.
Donc que le birapport (M,N,C,I) = -1, valeur conservée par l'homographie ayant envoyé C à l'infini.
Que D soit le milieu de AB, (A,B,∞,D) = -1, est d'ailleurs dans ce cas évident.
De toute façon, la projection de centre H de (M,N,C,I) sur la droite AB donne (A,B,C,D) = -1 dans le cas général.
D'où la construction cherchée :
On choisit un faisceau de droites HA,HB,HC issues d'un point H arbitraire
Tracer une sécante quelconque CEF, et les diagonales AE et CF se coupant en I
HI coupe AB en D cherché.
Concourantes ou parallèles
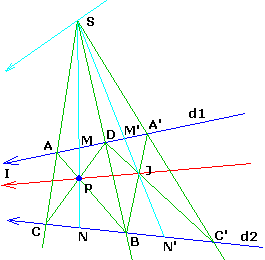Etant données deux droites d1 et d2 qui se coupent en I en dehors de la feuille (ou parallèles).
Par un point donné P tracer une droite concourante (ou parallèle).
C'est en fait la construction précédente (sa réciproque) effectuée deux fois :
la projection de centre I conserve le birapport (S,P,M,N) = (S,J,M',N') = -1, donc IPJ alignés.
Si I est à l'infini, les droites données sont parallèles mais la construction est la même.
Par P tracer deux sécantes AB et CD.
AC et BD se coupent en S
Une sécante quelconque SA'C', puis A'C et C'D se coupent en J.
PJ est la droite cherchée
Si P est sur la bisectrice (ou la parallèle médiane), S est à l'infini.
Il faut alors faire une première construction avec un point P' arbitraire pas sur cette bisectrice,
d'une droite concourante d'2 passant par P'.
On construit finalement la droite concourante à d1 et d'2 passant par P.
De même si P est proche de cette bisectrice, S serait à son tour en dehors de la feuille.
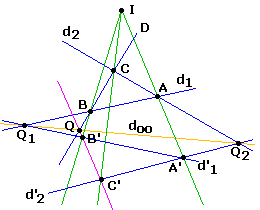Parallèles quelconques
• étant données deux paires de parallèles et une droite D,
construire une parallèle à D en un point P donné.
On est ici dans le cas où la droite de l'infini est déterminée par deux de ses points Q1 et Q2.
Une vue transformée par homographie de cette figure, où la droite de l'infini est "visible" :
Le théorème de Desargues
AA', BB', CC' concourantes en I ⇔ Q1 = AB∩A'B', Q2 = AC∩A'C', Q = BC∩B'C' alignés ici sur d∞ permet alors d'effectuer la construction sur cette figure d'une parallèle à D arbitraire, et on termine par la construction de la parallèle en P à ces deux droites.
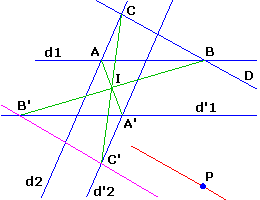Vue dans la figure de départ (où la droite de l'infini d∞ est à l'infini)
la construction devient même encore plus simple à comprendre :
(on peut la considérer comme une démonstration du théorème de Desargues !)
Soit I un point quelconque de la droite AA'.
B' l'intersection de IB avec d'1 et C' l'intersection de IC avec d'2
L'homothétie de centre I qui transforme A en A' transforme AB en A'B' ainsi que
AC en A'C' et finalement BC en B'C' qui sont ainsi parallèles.
Enfin la contruction de la parallèle en P aux deux droites parallèles D et B'C' n'est pas détaillée ici :
vue précédemment.
Points constructibles
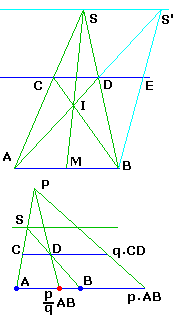
• étant donnés un segment AB et une droite parallèle,
construire le milieu de AB.
Là aussi, Thalès suffit dans un trapèze, déja vu.
Par un point S quelconque, tracer les sécantes SCA et SDB
BC et AD se coupent en I
SI coupe AB en son milieu.
On peut aussi dupliquer CD en DE (en construisant la troisième parallèle en S).
En construisant ainsi q×CD, et de même p×AB, puis par Thalès p/q×AB,
on peut alors construire tous les points à coordonnée rationnelle sur la droite AB,
le segment AB étant pris comme unité, et seulement ceux là.
Et par extension tous les points à coordonnées rationnelles
dans un repère affine défini par deux couples de droites parallèles
(par le parallélogramme "unité") et seulement ceux là.
Perpendiculaires
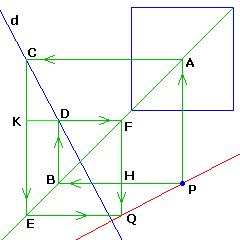Passons maintenant aux perpendiculaires...
Il faut bien entendu donner un angle droit quelque part !
• Etant donné un carré ABCD et une droite d. Construire en P la perpendiculaire à d.
Nous supposerons la droite pas déjà parallèle aux côtés du carré (évident) ni à ses diagonales (milieu des diagonales etc.)
Construisons (non détaillé mais vus précédemment) les parallèles en P aux côtés du carré, coupant la diagonale en A et B.
Les parallèles aux autres côtés en A et B coupent d en C et D.
Les parallèles aux premiers côtés en C et D coupent la diagonale en E et F
Enfin les parallèles aux autres côtés en E et F se coupent en Q.
Les triangles rectangles HPQ et KCD sont égaux (HP = KC et HQ = KD)
Les angles en P et C sont donc égaux et HP _|_ KC ⇒ PQ _|_ CD. CQFD.
Points constructibles
Dans le repère affine défini par ce carré (qui est certes orthonormé, mais c'est ici sans importance)
on ne peut construire que les points à coordonnées rationnelles.
Le point (1/√2, 1/√2) n'est donc pas constructible.
Bien que l'on puisse construire des angles droits, cela ne suffit pas encore.
La règle accompagnée
Montrer qu'avec un gobelet circulaire on peut construire à la règle seule (à un seul côté) et ce gobelet tous les points que l'on peut construire à la règle et au compas.Ceci est une application directe du "théorème de Cauer" :
| Tous les points constructibles à la règle et au compas sont constructible à la règle seule, étant donnés deux cercles sécants sans leur centres. |
Ce théorème se démontre (par la construction suivante) en le ramenant au théorème de Poncelet-Steiner :
| Tous les points constructibles à la règle et au compas sont constructible à la règle seule, étant donnés un cercle et son centre. |
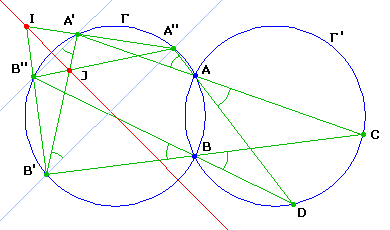On peut tracer avec le gobelet deux cercles sécants quelconques, de centre inconnu
(ils sont en fait égaux, mais sans importance ici) :
• Construire à la règle seule le centre de deux cercles sécants.
Choisissons sur un des cercles Γ' deux points C et D, sur l'arc extérieur.
<)CAD = CBD (angles inscrits)
AC recoupe l'autre cercle Γ en A', AD le recoupe en A", BC en B' et BD en B"
Les angles A"AA' et B"BB' sont donc égaux.
Les angles inscrits A'B'A" et B'A'B"
sont alors égaux et par conséquent A'B" et A"B' sont parallèles.
A'A"B'B" est donc un trapèze (isocèle car inscrit), les intersections de ses côtés non
parallèles A'A" et B'B" en I et de ses diagonales A'B' et A"B" en J
définissent son axe de symétrie IJ, donc un diamètre du cercle.
En recommençant la construction avec un autre choix de points (C, D),
on obtient un autre diamètre.
Le point d'intersection de ces diamètres est alors le centre du cercle.
Cette construction échoue si les deux cercles sont perpendiculaires :
le trapèze est alors un rectangle* et I est à l'infini.
Mais c'est alors bien plus simple :
Le centre du cercle est directement l'intersection J des diagonales !
* Preuve : prouver que l'angle en I ne dépend que de l'angle OAO'
Il reste qu'il vaut mieux éviter de loin cette orthogonalité en traçant avec notre gobelet les deux cercles sécants !
(Sinon I est trop loin)
En tout cas, même dans ce cas (I trop loin), on peut quand même tracer une troisième parallèle
formant ainsi un autre trapèze.
L'intersection des diagonales fonctionne toujours et donne un point J' et le diamètre JJ'.
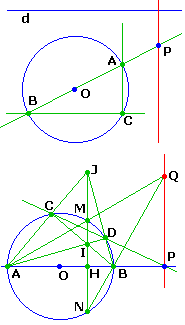Ensuite, ayant maintenant un cercle et son centre, on peut aisément construire des parallèles et perpendiculaires à volonté :
• Parallèles : la construction précédente donne deux paires de parallèles.
Sinon (si on part d'un cercle et son centre), deux diamètres quelconques donnent un rectangle,
donc deux couples de droites parallèles, et c'est gagné.
• Perpendiculaire à d en P.
Tracer OP coupant le cercle en A et B, puis la parallèle à d en B recoupe le cercle en C.
Enfin la parallèle à AC en P est la droite cherchée.
(la construction des parallèles n'est pas détaillée ici)
La construction échoue si OP est parallèle à d.
La construction de la perpendiculaire en P à OP peut être obtenue par la polaire du pied de la polaire de P :
construire la polaire de P (IJ), coupant OP en H, la polaire de H est la perpendiculaire cherchée.
Un seul point Q de cette polaire suffit, on connait déja P !
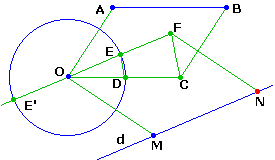• Reporter un segment donné AB sur une droite quelconque d à partir de M.
Tracer les parallèles à OA en B et à AB en O pour complèter le parallélogramme OABC
Soit D l'intersection de OC avec le cercle.
Tracer la parallèle à d en O, coupant le cercle en E E'
La parallèle à DE en C coupe EE' en F
La parallèle à OM en F coupe d en N, construisant ainsi MN = AB sur d,
à partir du point M donné.
Preuve : parallélogrammes et triangles isocèles semblables ODE et OCF.
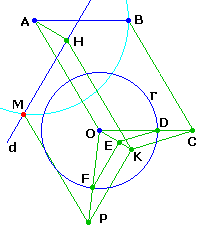• étant donnés deux points A et B et une droite d, construire les points
d'intersection de d avec le cercle (intraçable) de centre A et de rayon AB.
La clé est ici l'homothétie de centre O et de rapport AB/R.
Construire le parallélogramme OABC, et soit D l'intersection de AC avec le cercle donné Γ.
Construire la perpendiculaire AH à d en A.
Construire le parallélogramme OAHK.
La parallèle à CK en D coupe OK en E
La parallèle à d en E coupe Γ en F
La parallèle à d en K coupe OF en P
Complèter le parallélogramme HKPM
• étant donnés les points A,B et C,D construire les points d'intersection des cercles (intraçables) de centre A rayon AB et de centre C rayon CD.
La clé est ici la construction de l'axe radical des deux cercles.
On est alors ramené au problème précédent de l'intersection de cet axe radical avec un des cercles.
Théorème
| Soit I un centre d'homothétie des deux cercles.
Les polaires de I par rapport aux deux cercles sont symétriques par rapport à l'axe radical. |
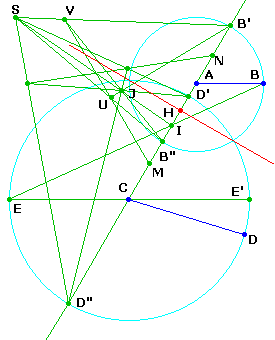Reportons les rayons sur la ligne des centres AC pour obtenir les diamètres B'B" et D'D"
Reportons l'un des rayons parallèlement à l'autre en CE pour obtenir un centre d'homothétie I.
En choisissant le centre d'homothétie négative, on s'assure que I n'est pas à l'infini
(si les deux cercles étaient égaux)
Construisons les conjugués harmoniques de I par rapport à B'B" et D'D"
Comme vu précédemment, tracer un faisceau (SB',SB",SI) issu d'un point S arbitraire.
Choisir un point J arbitraire sur SI.
B'J donne U et B"J donne V, enfin UV coupe B'B" en M, conjugué de I par rapport à B'B",
donc pied de la polaire de I par rapport au cercle de centre A.
Et de même pour N, pied de la polaire de I par rapport au cercle de centre C.
Le pied de l'axe radical est le milieu H de MN, et l'axe radical la perpendiculaire à AC en H.
On a ainsi prouvé que tous les points constructibles à la règle
et au compas sont constructibles à la règle et au gobelet.
Les dernières constructions proposées sont dans la pratique inutilisables, à cause de toutes ces
constructions de parallèles cachées sous le tapis et qui compliquent le tracé.
Nous allons donner maintenant des
Constructions classiques
Il s'agit ici de constructions à la règle seule classiques mettant en oeuvre un ou des cercles préalablement tracés.
Les premières constructions n'utilisent pas le centre du cercle, qui peut donc être inconnu.
Pole/polaire
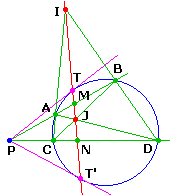Nous avons déja rencontré cette construction.
Rappelons la définition de la polaire de P : lieu des points conjugués harmoniques de P par rapport aux points d'intersection d'une sécante passant par P.
Ce lieu est une droite, et il suffit donc d'en trouver deux points.
Les propriétés du quadrilatère complet permettent de construire les conjugués M et N pour deux sécantes : la polaire est donc directement la droite IJ
En sens inverse (construire le pôle de d) on construit les polaires de deux points de d.
Le pôle de d est l'intersection de ces deux polaires.
Tangente issue de P
La polaire de P coupe le cercle aux points de contact des tangentes de P au cercle(la sécante variable devient la tangente quand A B M sont confondus en T)
Tangente en P
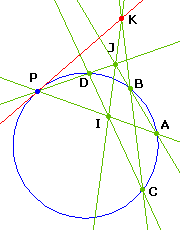La polaire de P est la tangente en P quand P est sur le cercle.
Par contre il est plus expéditif de construire la tangente en P par le théorème de Pascal. Les côtés opposés de l'hexagone PPABCD se coupent en trois points alignés (le "côté" PP est la tangente en P).
Pour la compréhension, distinguons P et P'
Les côtés opposés sont alors P'A et CD, se coupent en I
AB et PD se coupent en J
PP' et BC se coupent en K
PP' étant inconnu, on obtient ici K comme intersection de IJ et BC
PP' est donc la droite PK
L'hexagone PPABCD est ici croisé pour avoir I,J,K pas trop loin.
Inverse d'un point
L'inverse d'un point étant le pied de la polaire, la construction est immédiate. Il faut bien entendu connaître le centre du cercle pour construire l'intersection de cette polaire avec la droite OP.Une autre construction (déja vue) est de construire le conjugué harmonique de P par rapport au diamètre passant par P.
Centres de deux cercles non sécants
Hermite et Cauer ont montré (1912) que la donnée d'un seul cerle, ou de deux cercles non sécants (sans leur centre) ne suffit pas,il faut quelque chose de plus.
Christian Gram a alors prouvé (1956) qu'il est possible de construire leur centre étant donné un seul point A de la ligne des centres.
Cette construction est particulièrement complexe. Elle est donnée en Annexe (avec applets)
