Dissections de polygones réguliers

un hexagone en triangle équilatéral

L'aire de l'hexagone est 6×a/2×a√3/2 = 3a²√3/2.
En appelant c le côté du triangle équivalent :
 c/2×c√3/2 = √3/4 c² = 3√3/2 a²
soit c² = 6a² ou encore c/2 = a√3/2 × √2 qui permet de construire c/2.
Tracer HM = HF et DN = DI puis la médiatrice de IN coupe FM en P.
FM = IN = c/2, et le triangle INP est équilatéral. (PP' = IF/√2 etc...)
Le triangle cible est tracé en reportant IT = IP puis la parallèle TR à PN. Ses découpes internes sont obtenues en reportant MU = MA, MW = MF et enfin UV = UW.

La pièce ICBST est la symétrique de IODNP par rapport à I. La pièce MUW est la symétrique par rapport à M de MAF. Le triangle UVW est équilatéral (isocèle par construction et l'angle WUV = 60°) et égal au triangle COD. Comme FM est la moitié du côté du triangle et MW = FM par construction, FW = PR et la pièce WRSV est mise en place par translation de FPNE, de vecteur FW.

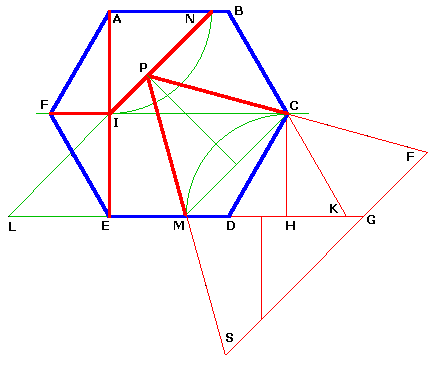Une autre construction plus ancienne, mais non optimale avec 6 pièces :
AN = AI, alors IN = AI√2 = AF√6/2 est la moitié du côté du triangle.
Construire de même HM = HC (soit CM = IN), puis P sur la médiatrice de CM.
La hauteur du triangle CMP est la distance entre les droites IN et MC à 45° de IC, donc cette hauteur est IC/√2 = 3a/(2√2) = (√3/2).(a√6/2) = MC√3/2.
Le triangle MCP est donc équilatéral : MP = PC = c/2
Tracer CF = CP et EF // MC pour compléter le triangle cible.
IEL symétrique de IAN et MGS symétrique de MLP
Les pièces AFI et FIE sont égales aux pièces CDH et HKC, enfin CFGK est le symétrique de CPNB

Hexagone en carré

La première dissection est celle indiquée par E. Lucas (1891)
L'hexagone AB'C'D'EF est coupé par un diamètre pour former un parallélogramme ACDF.
Le côté s du carré équivalent est la moyenne proportionnelle entre la longueur de ce parallélogramme et sa hauteur : s² = FI.FD
Tracer FH = FI, la perpendiculaire à FD en H coupe le cercle de diamètre FD en M. FM est le côté s du carré équivalent.
Compléter le carré FMNP. Tracer FK = UC (ou PK // CD)
Les triangles UWD et FHM sont semblables (angles à côtés perpendiculaires) et comme UW = FH, ils sont égaux et UD = FM = FP.
Le triangle FKP peut être ainsi obtenu par translation de UCD.
KP // CD // AF et égaux, les triangles PKV et FAG sont donc égaux par translation.
Enfin PV = FG donne VN = GM et les triangles VND et GMU sont égaux.

Nota important : là aussi des approximations douteuses sont à éviter. H et K ne sont pas confondus et FG n'est pas parallèle à EB.
FK = UC = WD – AI = HM – AI. Comme FM² = FH.FD = 3a²√3/2 = HM² + HF², HM² = 3a²√3/2 – 3a²/4 soit FK ≈ FH × 0,9924... là aussi de l'ordre de l'épaisseur du trait.
Quant à l'angle α = MFH, cos(α) = FH/FM donne a ≈ 57° 30'. Plus de 2° d'écart, c'est visible !

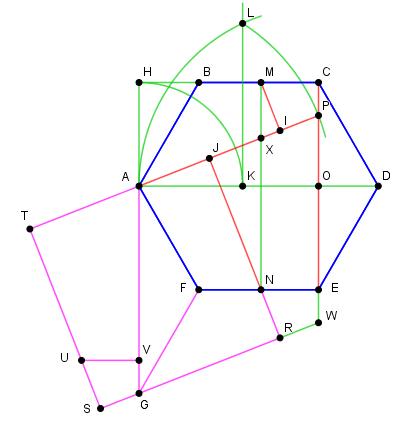Une autre dissection, qui permet de varier la forme des pièces (M draggable) :

Le côté du carré équivalent se construit comme ci-dessus : AK=AH
Puis L, intersection de la perpendiculaire en K à AD et du cercle de centre O de rayon OA = 3/2 a (diamètre = 3a donc).
Un cercle de centre A de rayon AL coupe CE en P.
Choisir une droite MN // CE quelconque, pas trop près de CE pour que le point I soit entre A et P, puis les perpendiculaires MI et NJ à AP.
Reporter JT = AP et compléter le carré TJRS.
MI + NJ est indépendant de la droite MN car MIX, NJX et AOP sont semblables MI/MX = NJ/NX = MI + NJ/MN = AO/AP et comme MN.AO = AP², MI + NJ = AP. Donc NR = MI.
Comme AG/JR = MX/MI = AP/AO, AG = MN = CE = PW et donc EW = CP, la pièce NEWR est donc égale à la pièce MCPI.
TAGS est égale à JPWR , avec ses deux morceaux.
AFG égale à CDE, et enfin GFNR est égale à ABMI.

On peut choisir MN librement, n'importe où comme ci-dessus,
ou bien pour que I = P, ou bien pour que F = N et M = B, ce qui donne trois formes différentes à cette dissection.

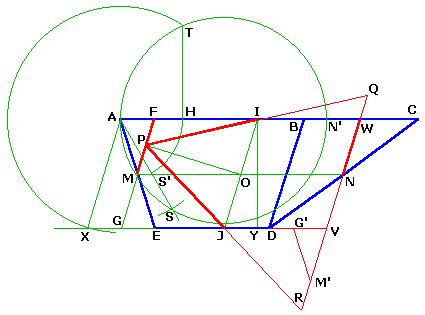Un pentagone en triangle
Soit 2c le côté du triangle équivalent. Sa surface est 1/2.2c.2c√3/2 = c²√3 = h.MN.
Traçons AN' = MN et le cercle de diamètre AN'. De A comme centre avec le même rayon, un arc de cercle le coupe en S, AS coupe MN en S'. AS' = h/√3.
Reporter AH = AS', la perpendiculaire en H à AB coupe le cercle de diamètre AN' en T : AT² = AH.AN' = h.MN/√3 = c². Le cercle de centre A de rayon AT coupe DE en X, le plus loin de E. AX = c. Tracer les parallèles FG à AX passant par M, WV par N et IJ par le milieu O de MN.
Tracer la perpendiculaire OP à FG à partir de O. Compléter la figure en traçant PIQ et PJR.
Nota important : les droites AX, FG, IJ et QR ne sont PAS parallèles à BD
En effet le calcul donne AX ≈ h × 1.04794... alors que BD ≈ h × 1.05146...
IJ = c par construction. Les triangles PIJ et PQR sont semblables QR/IJ = PQ/PI = MO/MN = 1/2, QR = 2c.
Les triangles POM et YIJ sont semblables, OP/IY = OM/IJ, soit OP = OM.IY/IJ = (MN/2).h/c = c√3/2. Le triangle PIJ a l'angle en I égal à 60° et est donc équilatéral, PI = PJ = c. Le triangle PQR est donc le triangle équilatéral équivalent cherché.
AFM et EGM symétrique de centre M sont égaux, les triangles GPJ et VRJ symétriques de centre J sont aussi égaux. Les triangles FIP et WIQ sont symétriques de centre I et enfin les triangles WCN et VDN sont symétriques de centre N. Tous les morceaux du pentagone s'assemblent ainsi dans le triangle PQR.

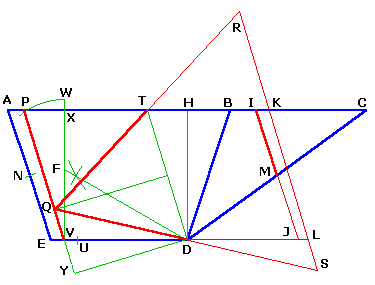Une autre dissection du pentagone en triangle :

Soit M le milieu de CD, IJ la parallèle à AE en M.
Reporter DU = DM, V le milieu de EU, la perpendiculaire à DE en V et DF tel que l'angle FDH soit 60° (les arcs de centres D et H et de rayon DH se coupent sur la droite DF)
Le cercle de centre F de rayon FV coupe AB en P. Tracer DT // VP.
La perpendiculaire à DT en son milieu coupe PV en Q.
Prolonger TR = TQ et DS = DQ.

DV = (ED + DU)/2 = MN/2. FDU = 30° donc FV = MN/2√3 et VW = MN/√3 soit VP² = VX.VW = h.MN/√3 = c demi côté du triangle équivalent.
Les triangles VDY et AVX sont semblables VD/AV = DY/VX soit DY = VD × VX / AV = MN/2 × h/c = c√3/2.
Le triangle DQT est donc équilatéral, QT = QD = c. Le triangle QRS double de celui-ci est donc le triangle équivalent au pentagone. De plus RS // TD.
Le triangle DMJ est le symétrique de centre M de CMI. l'angle MJD = 2π/5 et MDJ = π/5, donc DMJ = 2π/5, le triangle DMJ est isocèle et DM = DJ.
QVD est le symétrique de centre D de SLD, PTQ est symétrique de KTR.
Enfin JL = DL – DJ = DV – DU = UV = EV, AE // IJ, PV // KL et les pièces APVE et IKLJ sont donc égales.

Attention : PV n'est pas parallèle à AE.

Un pentagone en carré
Découper un pentagone régulier pour former un carré

Le "chapeau" (BCD) du pentagone est coupé pour donner un trapèze ACDE. Une bande formée par le carré équivalent est placée de sorte que ses bords passent par les milieux M et N des côtés du trapèze.

Reportons BF = MN et BI = BH = h, hauteur du trapèze.
La perpendiculaire en I à BF coupe le cercle de diamètre BF en J. BJ² = BI.BF = h.MN donne le côté du carré équivalent.
La perpendiculaire à BJ en B coupe DE en P. Tracer les perpendiculaires à BJ passant par M et N et la parallèle à BJ passant par P. Ceci construit le "carré" GSQR, reste à démontrer que tous ses côtés sont bien égaux à BJ car pour l'instant c'est seulement un rectangle.

Les triangles BJI et PBH sont semblables et même égaux puisque BI = BH, donc BP = BJ et SG = QR = BP par construction.
Les triangles BJI et MNT sont semblables, BJ/MN = BI/NT soit BJ.NT = MN.BI = h.MN = BJ²
Donc NT = BJ et QS = GR = NT = BJ. C'est bien le carré équivalent.
Les triangles MAK et MEU sont égaux, symétriques par rapport à M, UK = PB = GS donc UG = KS et les triangles UGP et KSB sont égaux. UGP se compose des deux pièces UME et MGPE.
Nota important : G et M ne sont pas confondus, MGPE est un vrai quadrilatère, même si son côté MG est tout petit.
Les triangles NWC et NVD sont égaux par symétrie de centre N.
GP = SB donc PR = BQ et les triangles BWQ et PVR sont égaux.
Toutes les pièces du pentagone trouvent ainsi leur place dans le carré.

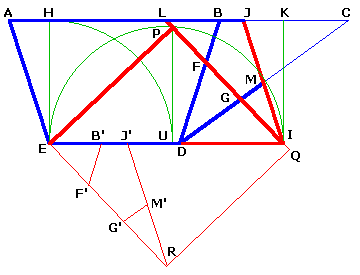Lucas proposait la dissection du pentagone en carré avec 7 morceaux. Celle-ci a donc un intérêt purement historique.

Le "chapeau" BCD du pentagone est coupé pour donner le trapèze ACDE.
La parallèle IJ à AE passant par le milieu M de CD donne le parallélogramme équivalent AJIE.
Reporter EU = EH, hauteur du parallélogramme.
La perpendiculaire à EI en U coupe le cercle de diamètre EI en P. IP coupe AB en L. Compléter le carré EPQR.
EP² = EU.ED donne le côté du carré équivalent, moyenne proportionnelle entre la base EI et la hauteur EU = EH.
Les triangles EPU et ILK sont semblables, et puisque EU = IK, ils sont égaux et donc IL = EP = PQ.
Soit J'R la parallèle à JI en R. Les triangles EJ'R et LJI sont semblables, et égaux puisque ER = IL
Comme IL = PQ, PL = IQ. Les morceaux ALPE et J'IQR sont donc égaux, tous les morceaux du pentagone s'assemblent bien dans le carré.

Les polygones à 7, 9, 11 côtés ne sont pas constructibles à la règle et au compas, et ne nous intéresseront donc pas.
Restons dans les dissections en triangles et carré et reposons nous avec la dissection de l'octogone en carré.

Octogone en carré

Soient M, N, I, J les milieux de côtés opposés de l'octogone.
Il s'agit de construire un carré de côté celui de l'octogone, et passant par M,N,I,J.
C'est à dire de construire deux parallèles MA et NC à distance = c, côté de l'octogone.
Le cercle de diamètre MN et le cercle de rayon c se coupent en P.
MP est la droite MA cherchée, et les 4 autres s'en déduisent immédiatement.

La preuve est immédiate par translation des pièces, et les conditions évidentes d'angle, de symétrie et d'égalités des segments.

Cette dissection est issue d'un pavage avec des octogones + un carré de côté c, superposé à un pavage de carrés équivallents + carrés de côté c.

Attention : P n'est pas le milieu d'un côté ! et donc MP n'est pas parallèle à la diagonale de l'octogone.

Octogone en triangle

Comparativement, la dissection de l'octogone en triangle est beaucoup plus compliquée.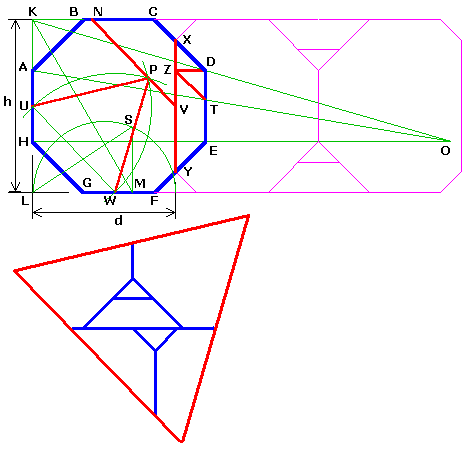

Cette dissection passe par la transformation de l'octogone en une bande périodique. La condition ZT = TE = EY donne ET/ED = HA/HK et la construction de cette découpe par une homothétie de centre O, intersection de HE et KD.
L'aire de l'octogone est alors simplement la moitié de l'aire d'un motif complet (2 octogones) de cette bande. Soit d×h.
On peut alors facilement construire le côté du triangle équivallent.
Le côté s de ce triangle est donné par  s²√3/4 = d×h soit  (s/2)² = d.h/√3
La droite KM issue du coin du carré circonscrit à l'octogone, à 30° de la verticale, donne LM = h/√3. Un cercle de diamètre d coupe la verticale MS en S et LS est le demi côté du triangle équivallent.
Soit U le milieu de AH.
Construire le triangle équilatéral PWU, puis la parallèle NV à UW en P.

On se méfiera particulièrement des points qui ne sont PAS aux milieux de segments. En particulier W n'est pas au milieu de FG : WG < WF, et donc NV et UW ne sont pas parallèles à GH.
Ceci a pour conséquence que la pièce NCXV n'est pas un trapèze.
Par contre V est bien le milieu de XT, et NV = UW.
La façon la plus expéditive de le prouver est par repliement des pièces sur le pavage, compte tenu que le triangle ainsi construit est équilatéral par construction et a effectivement même aire que l'octogone, par construction.

Décagone en carré

La dissection suivante conduit à des pièces "bizarrres", mais c'est le minimum (7 morceaux). Découverte par Gavin Theobald.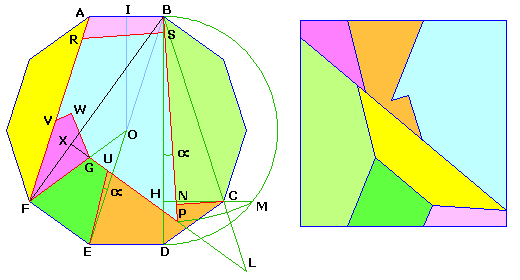

Soit I le milieu de AB = a, la surface du décagone est 20× celle du triangle OIB. 20 exemplaires de ce triangle peuvent donc remplir un rectangle de côtés BD et BH = 5×BI. La perpendiculaire en H à BD coupe le cercle de diamètre BD en M. BM est la moyenne proportionnelle entre BH et BD et est donc le côté du carré équivalent.

Traçons FG = FE sur le rayon OF et GL parallèle à EF, L étant l'intersection de cette parallèle avec BC.
Le cercle de centre B de rayon BM coupe la droite GL en P. Tracer CN perpendiculaire à BP.
Tracer FV = LP. Les cercles de centre V de rayon PN et de centre G de rayon CN se coupent en W, soit VW = PN et GW = CN.
Tracer EU tel que l'angle UEO avec le rayon EO soit égal à l'angle NBD = α
Reporter AR = GU et tracer la perpendiculaire RS à BP.

Pour justifier le remplissage du carré, outre les considérations d'angles, les segments égaux aux côtés du décagone et les segments qui sont égaux par construction, il reste à démontrer que LC = FG = a.
BF _|_ GL coupe GL en X. BF = 2a(sin(π/5) + cos(π/10)), FX = a cos(π/10) donc BX = a(2sin(π/5) + cos(π/10)).
BC = a(1 + 2cos(π/5)) et BX = BL sin(π/5) = CL sin(π/5) + BC sin(π/5) = CL sin(π/5) + a sin(π/5) + 2a cos(π/5)sinπ/5) et comme 2cos(π/5)sin(π/5) = sin(2π/5) = –cos(π/10), CL est bien égal à a.

Nota : la perpendiculaire en H ne passe PAS par C.
En effet la projection de BC = a(1 + 2cos(π/5)) sur BD est a(1 + 2cos(π/5))cos(π/10) ≈ a×2.489... ≠ 5a/2

Dodécagone en carré

Encore une dissection "facile" !
Sans commentaires...

Les dissections du décagone et du dodécagone en triangle sont assez "horribles*" et nous n'en parlerons pas, nous contentons ici de dissections relativement abordables.
* la difficulté étant le découpage "étrange" pour transformer ici le n-gone en bande !
On trouvera sur le site de Gavin Theobald de nombreuses autres dissections. Y compris de n-gones en p-gones avec n, p > 4.

En restant encore dans des dissections "abordables", nous allons construire la dissection du pentagone en hexagone :

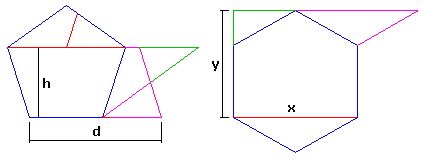Pentagone en hexagone

Partons d'une dissection déja vue du pentagone en parallélogramme et de la dissection de l'hexagone en bande. La méthode des bandes donne alors par superposition la dissection cherchée (H. Lindgren 1964).
L'aire de l'hexagone est xy = x²√3/2 on doit donc avoir dh = x²√3/2. Soit x² = d × 2h/√3
Il s'agit donc de construire, étant donné le pentagone, le côté x du rectangle équivallent à l'hexagone.

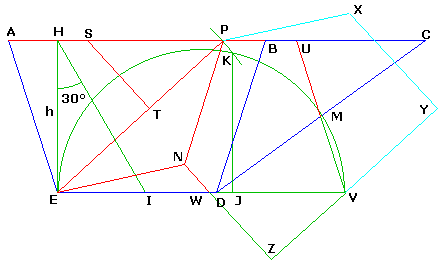Construisons EI = h/√3 et donc EJ = 2h/√3, alors x² = EI.EV donne la construction de x : La perpendiculaire en J coupe le cercle de diamètre EV en K. EP = EK = x
Complèter le chapeau EPN de l'hexagone, et le morceau d'hexagone NPXYZ. NZ _|_ EP et YZ passe par V (bandes, aires égales etc.) rendent inutile le tracé effectif de X,Y : la perpendiculaire NZ à EP en N coupe ED en W. Enfin WVZ est recopié en SPT pour donner la dernière découpe ST (PS = VW et ST _|_ EP).

7 pièces suffisent donc, ce qui est exceptionnel pour une transformation de n-gone en p-gone..

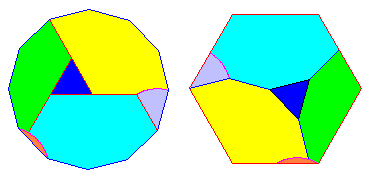Une autre dissection de n-gone en p-gone abordable est celle de l'hexagone en dodécagone avec 6 pièces seulement. par adjonction d'un triangle équilatéral pour obtenir un pavage hexagone + triangles superposé à un pavage dodécagone + triangles (comme pour l'octogone en carré vu plus haut).
Malheureusement une des pièces est minuscule, l'astuce est d'utiliser des pièces courbes par exemple (en magenta).
La méthode pour élaborer cette construction est de considérer le lieu du point T et de choisir T pour que les triangles ajoutés soient tous égaux.

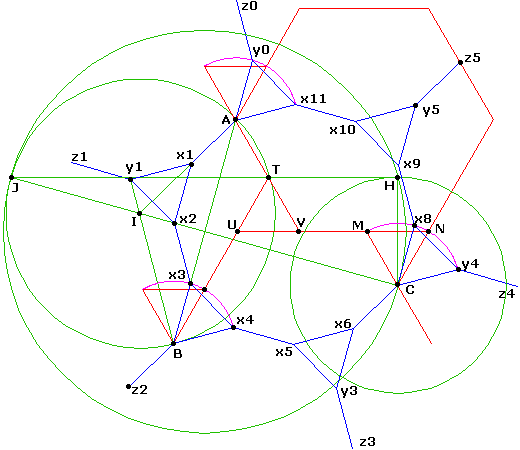L'angle ATB étant de 120°, T est sur un cercle de centre I, intersection de Ax1 et By1 (arc capable).
La bisecrice de l'angle ATB passe par J, milieu de l'arc AB extérieur, et point d'intersection de la médiatrice Cx2 de AB avec ce cercle.
Pour que les triangles TUV et CMN soient égaux, et égaux au triangle ajouté, la distance de C à JT doit être le double de la hauteur h de ce triangle.
On construit donc le point H intersection du cercle de diamètre JC avec le cercle de centre C de rayon 2h. JH coupe l'arc capable en T cherché.
La suite de la construction est triviale.
On obtient alors au voisinage de N une pièce triangulaire minuscule.
Cette pièce est remplacée par une de taille raisonable en remplaçant les triangles en A, B, C par des triangles à côtés curviligne : CMN est la rotation de centre C du triangle Cx8y4, l'arc de cercle est ainsi de centre C et de rayon Cy4 = Cx8 = CN = CM.

Nota : z5 est sur le côté de l'hexagone, c'est la translation de B de module z2y5^> (maille du pavage)

Les amateurs de calcul pourront vérifier que :
- JT ne passe pas par y1
- AT n'est pas un rayon (ne passe pas par le centre du dodécagone, ni par x6)
- UV n'est pas parallèle à l'axe du dodécagone x2x8