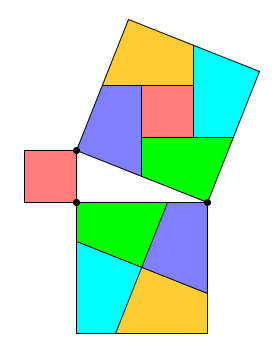
Dissection d'un carré en deux carrés

Désolé, votre navigateur n'est pas compatible Java. Il y a plusieurs dissections "classiques" d'un carré en deux carrés.
Une très connue est la dissection symétrique prouvant le théorème de Pythagore.
Si les deux carrés sont égaux, les 4 pièces deviennent des triangles rectangle isocèles (découpe selon les diagonales d'un des carrés).
Evidemment dans ce cas ce n'est pas la meilleure découpe possible, car il suffit de 4 pièces !

Il est possible de réaliser cete dissection avec des pièces "articulées" entre elles.
Nota : dans l'animation ci-contre, les pièces extrèmes tournent trop vite et suggèrent une collision. Si on fait tourner les pièces une par une, il n'y a pas de collision.
Une rotation individuelle automatique des pièces est trop compliquée.

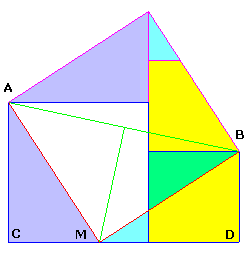Une autre façon de procéder est de placer les deux carrés côte à côte

MC = BD et donc MD = AC. Les triangles rectangles ACM et MDB sont égaux, MA = MB et se déduisent l'un de l'autre par rotation autour du milieu de AB. Donc MA _|_ MB.
MA² = AC² + MC² est alors le côté du carré de surface égale à la somme des carrés de côté AC et BD.
Cette construction est toujours possible. Au pire les deux carrés sont égaux, M au milieu de CD et la petite pièce triangulaire disparaît.
Nota : cette dissection est aussi articulée.

La construction de la découpe à partir du grand carré est laissée au lecteur.
On s'intéressera plus particulièrement au problème posé par E. Lucas :
Découper un carré en deux carrés dont l'un a une aire double de l'autre.

Cas particuliers

Dans certains cas, la dissection peut se faire en 4 pièces seulement.

Carré de 5×5 en 3×3 + 4×4

Il existe même de nombreuses dissections possibles
Lors de discussions sur de.rec.denksport, "Quadrat zerschneiden" il a été trouvé 72 solutions.
Bien entendu on ne distingue pas les dissections obtenues par rotations ou symétries.
Les pièces sont classées par ordre "lexicographique".
De gauche à droite et de bas en haut, on nomme A la première pièce rencontrée, puis B la suivante etc.
La dissection N° 3 ci-dessous est ainsi représentée

AAAAB
AAAAB
AAAAB
CCCAD
CCDDD

soit AAAAB.AAAAB.AAAAB.CCCAD.CCDDD
On choisit alors parmi les symétries et rotations la représentation de cette découpe qui est la première par ordre alphabétique.
Ici les autres pour la même découpe commenceraient par AAABB... ou AABBB...

Les couleurs ont été affectées ainsi :
vert le premier plus gros morceau du carré 4×4
mauve le premier plus gros morceau du carré 3×3
jaune le premier plus gros morceau restant
rouge le reliquat
Les pièces entourées en gras doivent être retournées (les premières plus petites pièces à retourner).

En fait, on peut même obtenir des familles infinies de solutions par des découpes obliques :

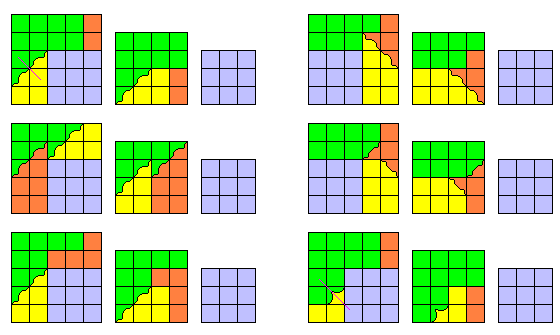
Il suffit de choisir une ligne de séparation quelconque, symétrique par rapport à la diagonale.
Le retournement de la pièce jaune (symétrie par rapport à cette diagonale) laisse ainsi la forme de la séparation inchangée : les deux pièces s'ajustent.
Bien entendu on peut se limiter à des "courbes" selon une subdivision du quadrillage, simplement avec des segments horizontaux et verticaux.

Et ensuite...

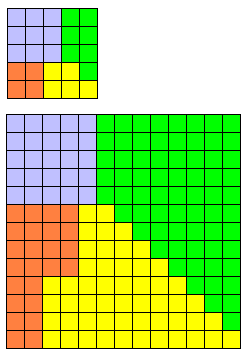On peut imaginer que tout triplet de Pythagore donne une telle dissection en 4 pièces seulement.
Partons de la dissection N° 51 ci-dessus.
On peut la généraliser aux triplets de Pythagore suivants.
5² + 12² = 13² donne la méthode.
Evidemment dans le cas de 3² + 4² = 5², l'escalier à une seule marche n'est pas très visible !
Le triplet 7² + 24² = 25² est encore plus démonstratif de la méthode.

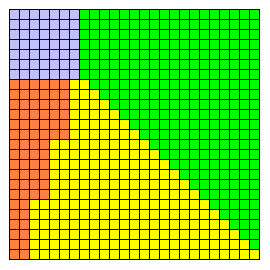
Cette méthode n'est pas la seule. Elle n'est valable que pour les triplets de la forme a² + b² = (a+1)².
Deux autres variantes, dérivées de la dissection N° 17 du 5×5 :

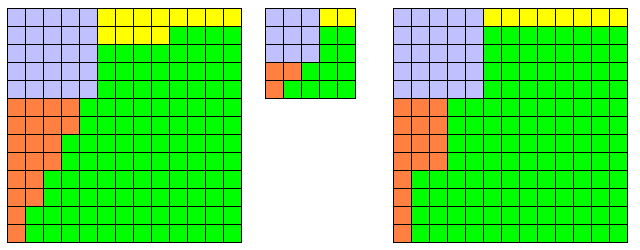
Elle ne fonctionne plus pour 8² + 15² = 17²
Une variante d'escalier à "marches rentrantes" donne toutefois une solution :

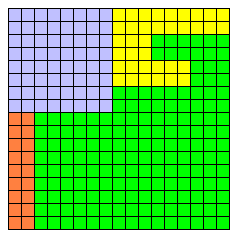
Extensible à d'autres triplets du même type, par exemple 37² = 12² + 35²

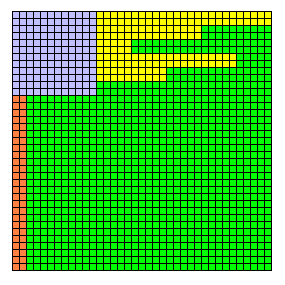
Le premier triplet non résolu par les méthodes précédentes est 29² = 20² + 21² le suivant 53² = 28² + 45²

Preuve que la découpe du 13×13 fonctionne pour tous les triplets de la "famille de Pythagore" (c = a+1) et pas pour les autres.
[...]

Preuve que la découpe du 17×17 fonctionne pour tous les triplets de la "famille de Platon" (c = b+2) et pas pour les autres.
[...]