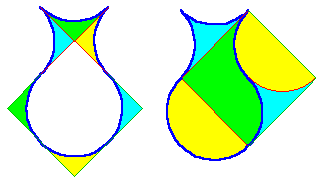Formes courbes

Commençons par le vase ... évident.
Bien entendu on oubliera la dissection en 4 pièces pour ne conserver que celle moins visible en 3 pièces seulement !

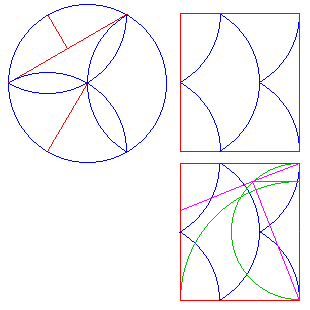Le cercle évidé se résoud de même, puisque la longueur courbe totale est nulle : il y a autant de longueur d'arcs concaves que d'arcs convexes, tous de même rayon. Il est ainsi évident d'obtenir un rectangle en quelques coups de ciseaux.
Reste à le transformer en carré... par les méthodes usuelles, et reporter les dissections sur le cercle.

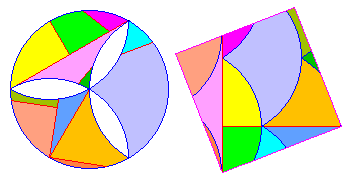
Le challenge est maintenant de faire cette dissection en moins de 12 pièces !
Il faut noter que ce cercle évidé a pour aire visiblement (par une autre dissection) la même que celle de l'hexagone inscrit.

Croissant en carré

On peut certes dupliquer le croissant pour former une bande, mais la largeur de cette bande étant supérieure aux dimensions du carré équivallent, cela ne marche pas aussi simplement.
La forme exacte du croissant influe sur le découpage. On considère ici deux formes de croissant :
• Le croissant "de Sam Loyd", hauteur 5×largeur, arcs < 180°
• Le croissant "de Dudeney", demi cercles, hauteur = diamètre = 4× largeur.

Pour transformer en carré, le croissant de Dudeney semble idéal : il suffit de superposer le carré avec une bande formées de demi-croissants. On obtient ainsi la dissection en 4 pièces seulement. Facile...

Le croissant de Sam Loyd résiste un peu plus.
Toutefois la dissection de deux carrés de 2×2 + 1×1 en un seul donne la surface équivalente de 5 unités. Le recouvrement de la bande de croissants par la bande de paires de carrés, munis de leur propre dissection en un seul (A-M-B), donne ainsi une dissection en 8 morceaux.
Pour que cette dissection fonctionne, encore faut-il que les deux bandes soient positionnées correctement.
Un minimum de pièces est ainsi obtenu lorsque l'axe est équitablement divisé par les motifs de carrés et de croissants. C'est à dire le croissant passe par le point W.

L'applet montre ce phénomène :
Les croissants peuvent être décalés en déplaçant le point jaune, initialement en W.
On peut choisir la valeur de l'arc en choisissant le centre I du cercle.
La limite étant le demi-cercle de diamètre 5 fois la largeur du croissant, "à la Dudeney".
Le point M vient alors précisément sur une copie du croissant (3² + 4² = 5²)
Si le rayon du cercle augmente, M n'est plus exactement sur le cercle, et la pièce MBP'M' possède alors un tout petit côté MM' ≠ 0.
Lorsque, en augmentant le rayon, P, voire P", vient en B, il y a une pièce de moins.
Pour les grandes valeurs du rayon du cercle, le croissant ne ressemble plus tellement à un croissant d'ailleurs...
Le croissant précisément défini par Sam Loyd a un rayon =  √26/2 fois la largeur. (bouton "Sam Loyd" dans l'applet)
(c'est pour faire fonctionner correctement la dissection en croix grecque).

Gavin Theobald a trouvé une dissection en 7 pièces seulement du croissant de Sam Loyd en carré.
On peut se poser la question pourquoi une telle dissection n'a pas été trouvée plus tôt, tout le monde était sans doute obnubilé par les 5 carrés.
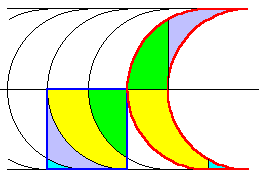
Quoi qu'il en soit, après coup cette dissection semble naturelle : Il "suffit" de superposer la bande de 1/2 croissants avec une bande de rectangles équivallents.
La dissection du rectangle en carré équivallent est alors "comme d'hab" avec un P-slide.
Ici aussi, cette dissection donne lieu à une infinité de variantes selon le décalage des bandes (et selon le rayon du croissant)
L'applet suivante montre cette dissection "en action".
Le point I définit le rayon du croissant.
Le point jaune décale les croissants par rapport au rectangle ABCD
La position initiale de l'applet correspond au croissant de Sam Loyd et à la dissection de Gavin Theobald. (taper R pour revenir à cette position initiale)
La découpe en 7 morceaux fonctionne tant que les découpes du P-slide (en rouge) n'interfèrent pas avec les bords des croissants.

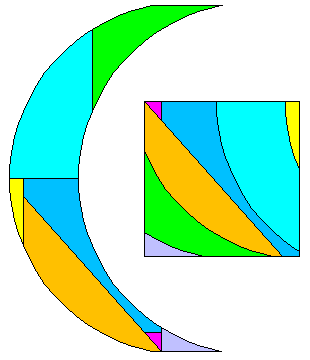
La même technique s'applique si la hauteur est ≠ 5×largeur (le point B est draggable).
Elle peut être alors intéressante ... ou non.
Pour le croissant de Dudeney (h = 2R = 4d) le rectangle est même ... directement le carré équivallent !
Pour h ≤ 4d le P-slide disparait purement et simplement, il faudrait le faire dans l'autre sens.

Croissant en croix grecque

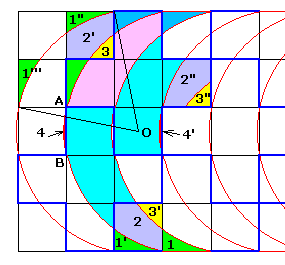
La croix grecque étant composée de 5 carrés unités, le croissant de Sam Loyd (hauteur = 5× largeur) est idéal.
Le croissant devant passer par les points du quadrillage, son rayon est R² = 0.5² + 2.5² = 26/4 soit le R =  √26/2 annoncé.
La construction et sa preuve est directe sur la figure.
Il suffit de remarquer que la pointe 1 du croissant est égale (translation) à 1' et que le carré 1' 2 3' identique (symétrie glissée) au carré 1"2'3. La pièce 3 du croissant complète donc ce carré. Comme 1" = 1''' (symétrie à 45°), les pièces 2 et 3 du croissant viennent bien en 2"3" de la croix (translation du reste du carré contenant 1''').
Le reste des pièces est trivial.

On n'oubliera pas la pièce 4, minuscule petit bout qui dépasse et que l'on met de l'autre côté en 4'.
Soit 7 pièces en tout.

 

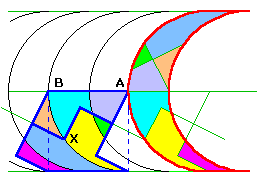
Le croissant de Dudeney se dissèque en croix grecque en remplaçant la bande de carrés par une bande de même largeur de croix équivallentes. Le carré équivallent est tracé en pointillés.
Pour prouver la dissection, il suffit de prouver que X est sur le cercle.
C'est à dire que AX = AB, ce qui est à peu près évident compte tenu de la dissection du carré en croix grecque.

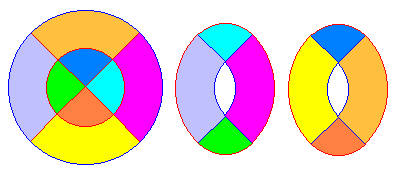Table ronde

La difficulté ici est bien entendu qu'il n'y a aucun arc concave dans le disque de départ.
Une solution bien connue et (trop) facile découpe la table ronde en 8 morceaux.
Sam Loyd dans son "Cyclopedia of 5000 puzzles" trouve une dissection en 6 morceaux seulement, en utilisant astucieusement le taijitu ou monade (Yin et Yang).
Tous les arcs ont pour rayon R/2 et sont des demi ou quarts de cercle.

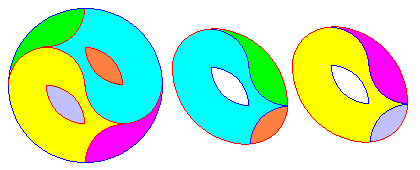
Il existe d'autres dissections en 6 pièces, et même des dissections en 5 pieces seulement sur le site de Greg Frederickson's
Une variante avec le trou disposé autrement, en 4 pièces seulement :

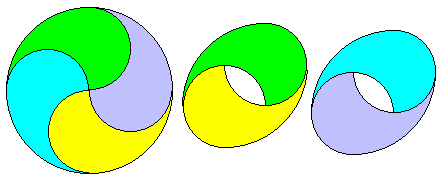
Fleurs

Des formes biscornues peuvent donner lieu à des dissections évidentes ... une fois qu'on a vu où couper !
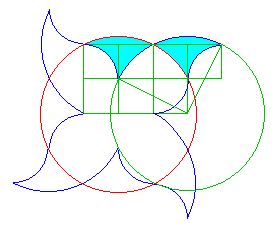
Ainsi une fleur à 4 pétales en un cercle.
Le quadrillage sert de construction et de preuve de cette dissection. Sans plus de commentaires.

Si on cherche à généraliser à un nombre différent de pétales, la difficulté est bien plus grande pour obtenir une construction correcte.

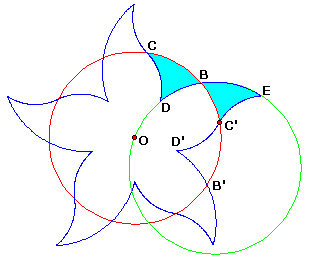Cherchons directement avec n pétales, ici n = 5.

Bien qu'il puisse exister d'autres sortes de fleurs (comme dans l'exemple avec n = 4 ci-dessus), nous prendrons comme hypothèses que le grand arc de cercle passe par le centre de la fleur, et que les deux petits sont symétriques par rapport à leur point commun, situé sur le cercle équivallent.
Bien entendu le grand cercle vert et le cercle équivallent rouge ont même rayon.
Les arcs DB = BC' et BE = CB entraînent que l'arc DE = CC' = 2π/5 (2π/n dans le cas général).
Enfin D' se déduit de D par rotation de 2π/5, et de plus C' est le milieu de D'E
Ces dernières conditions déterminent de façon unique l'emplacement de D sur le cercle ODBE, et les autres points s'en déduisent alors aisément.
Les petits arcs ont un rayon quelconque, sans que ça déborde tout de même...

Entrons un peu plus dans le détail de cette construction avec une applet Geogebra permettant de faire varier l'arc C'D' (de centre Ω) et n variable.
Le cas n = 2 (un digone) n'est pas traité, mais la construction se simplifie fortement dans ce cas : D et D' viennent en O et les arcs sont des demi-cercles !

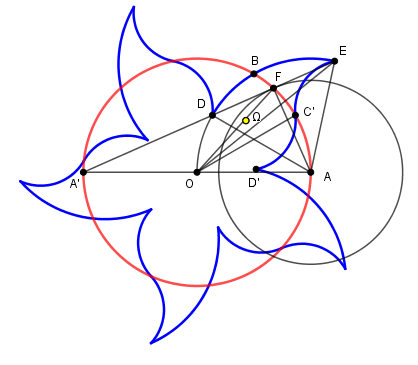
Soit A le centre du cercle ODBE, on a donc <)DAE = 2π/n, et <)DOE = DAE/2 (angle inscrit)
Comme <)DOD' = 2π/n itou, on en déduit que OD' est symétrique de OD par rapport à la droite OE.
Le milieu C' de D'E est donc le symétrique de F milieu de DE, d'où la construction :
Construire l'apothème a du n-gone inscrit, un cercle de centre A et de rayon a coupe le cercle équivallent (rouge) en F, puis DE _|_ AF donne DE = côté du n-gone (donc DAE = 2π/n) et F milieu de DE.
Les autres points se construisent alors immédiatement à partir de D et E.
Reste à justifier la dissection en prouvant que l'arc BC' ainsi construit est égal à l'arc BD.

Soit A' le point diamétralement opposé à A
Donc A'DFE alignés (AFA' = π/2)
Posons α = <)FA'O, et bien entendu <)A'FO = α (A'OF isocèle) et <)FOA = 2α (angle inscrit).
Posons β = <)DEO, ici aussi <)DAO = 2β
Dans le triangle FOE, <)FOE = π - β - (π - α) = α - β
<)C'OA = <)FOA - 2<)FOE = 2α - 2(α - β) = 2β
Les angles <)C'OA et <)DAO sont donc égaux, les arcs OD et AC' aussi donc, et finalement les arcs BD = BO - OD et BC' = BA - AC' sont égaux. CQFD.