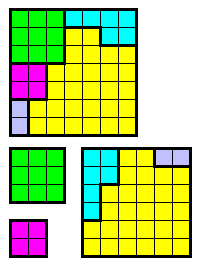
3 carrés en un seul

Nous avons déja vu la dissection de 3 carrés égaux en un seul (6 morceaux), et de 3 carrés d'aires 2:3:4 en un seul (7 morceaux).
Il y a même des dissections rationnelles, telle celle de Sam Loyd pour 2² + 3² + 6² = 7², qui se font en 5 morceaux seulement.

Etudions le cas général.
Greg N. Frederickson a affirmé ("Dissections : Plane & Fancy") que ce cas général est toujours possible en 8 morceaux. "I identify three cases that cover all possibilities [...]"
Nous reprendrons son étude, mais dans l'autre sens ce qui semble à mon avis plus logique, et permettra de prouver que sa conclusion est erronée : il existe des cas où ses dissections en 8 pièces ne suffisent pas.

Soit donc x² + y² + z² = w², x ≤ y ≤ z (et bien sûr < w !)
Normalisant la taille à w = 1 on obtient x² + y² + z² = 1 et la forme de la figure est entièrement définie par (x,y). Les différents cas seront ainsi repèrés dans le plan xOy.

En relaxant la contrainte x ≤ y ≤ z, on a bien entendu x² + y² < 1 et le quart de cercle correspondant
La valeur de z dans ce diagramme est d'ailleurs repérée par le rayon des cercles concentriques x² + y² = 1 - z²

x ≤ y est bien entendu au dessus de la droite à 45°
y ≤ z rajoute la contrainte x² + 2y² ≤ 1 et le quart d'ellipse correspondant.

En fait seul le secteur d'ellipse coloré est utile et détermine tous les points possibles de façon unique. Les autres régions sont les autres cas x : y : z.

Découpe en deux rectangles

La méthode la plus simple est de placer le carré de côté x, non découpé, dans un angle du carré de côté w.
Les carrés de côtés y et z sont transformés en rectangles équivallents que l'on place "au mieux". C'est à dire avec un côté = w - x et donc l'autre respectivement égal à y²/(w - x) et z²/(w - x).
La dissection de ces rectangles en carré est effectuée "comme d'hab" en 3 morceaux.
En fait, rien n'impose dans cette dissection d'avoir x < y < z.
Ou ce qui revient au même, en gardant x < y < z on peut en fait choisir le carré non découpé comme x, y ou z.
En tout état de cause nous conservons le nom z au plus grand des deux carrés restant.
Le domaine de définition de cette dissection est ainsi avec la seule contrainte y < z, et x sera le carré non découpé (pouvant être ainsi > y ou z).
In fine, les notations seront "normalisées" en ramenant les domaines concernés à x < y < z par changement de variables.

L'applet ci-dessous montre cette dissection dans les cas où c'est possible.
Les points déplaçables X et Y définissent les côtés des carrés correspondant.
L'applet en déduit Z et la dissection, et reporte le point de coordonnées (x,y) sur le graphe.
Les points déplaçables O,0,1 définissent le cadrage et l'échelle.
En grisé les points reportés après changement de variable (x,y) → (y,x) (pour y<x<z) ou (x,y) → (y,z) (pour y<z<x)

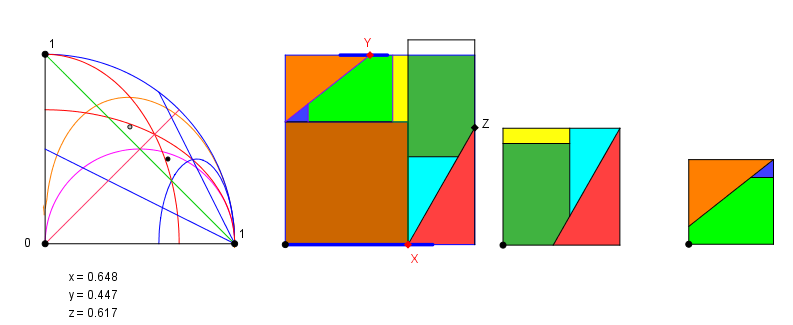
Il y a alors deux cas à envisager :

1. Les deux rectangles, tous deux intérieurs à w², se recouvrent partiellement
   C'est à dire la longueur du rectangle y²/(w - x) est > x, soit la condition y² > x(w - x) ou encore après simplification :
   (2x - 1)² + 4y² > 1 à l'extérieur du demi cercle de diamètre (0,0)-(1,0).
   La surface commune étant bien entendu égale à la surface non recouverte du carré w², ce morceau est alors découpé de l'un des rectangles et déplacé pour boucher le manque du grand carré.

2. Un des rectangles (le plus grand, donc = z²) déborde de w². C'est à dire (x,y) à l'intérieur du demi-cercle précité.
   Le morceau qui déborde est alors découpé et remis en complément dans le carré w²

La dissection des rectangles dépend de l'orientation de ceux-ci :
Rectangle z² vertical si z > w - x, ou encore (2x - 1)² + 2y² - 1 < 0 matérialisé par l'ellipse en noir.
Le rectangle z² est horizontal à l'intérieur de cette ellipse.
De même le rectangle y² est horizontal si y > w - x, matérialisé par la droite x + y = 1

La dissection en 3 pièces n'est possible que si le rapport des côtés est < 4:1
Rectangle y², de dimensions w - x et y²/(w - x) :
(w - x)/4 < y²/(w - x) < 4(w - x) soit entre les droites x + 2y = 1 et x + y/2 = 1

Rectangle z², de dimensions w - x et z²/(w - x) :
avec z² = w² - (x² + y²) = 1 - x² - y²
(1 - x)/4 < (1 - x² - y²)/(1 - x) < 4(1 - x)
La première condition donne après simplification l'intérieur de l'ellipse (5x - 1)² + 20y² - 16 = 0,
qui pour x > 0 est extérieure au domaine de définition y < z.
Même la condition plus restrictive (1 - x)/2 < (1 - x² - y²)/(1 - x) (ratio < 2:1) conduit à l'intérieur de l'ellipse (3x - 1)² +6y² - 4 = 0, elle aussi contenant tout le domaine de définition.

Il est toujours possible de dissèquer le rectangle z² horizontal

La seconde donne (5x - 4)² + 5y² - 1 > 0 soit à l'extérieur de l'ellipse correspondante.
Cette ellipse a pour petit axe (3/5,0)-((1,0) et par conséquent :

Il est toujours possible de dissèquer le rectangle z² vertical si x<y<z

Le problème ne se pose ainsi que si x>y.

La construction dans le cas des rectangles superposés échoue si la partie commune interfère avec la dissection d'un rectangle en carré.
Ceci ne se produit jamais si le rectangle d'aire z² est "vertical".
Au mieux dans le cas où ce rectangle est horizontal, on n'utilise bien sûr pas le P-slide proposé par Frederickson, mais la dissection vue par ailleurs (P-strip). Cette dissection n'est possible que si le rapport des côtés est < 2:1 ce qui comme on l'a vu est toujours vrai.

La dissection P-strip du rectangle z² horizontal est toujours possible

Cette dissection retarde un peu le conflit, mais ne l'évite pas.
La frontière est obtenue en écrivant que le coin du rectangle de recouvrement, de coordonnées (y²/(w - x), x) est sur la découpe du rectangle d'aire y², de pente √(w - x)² - z² / z, en tenant compte que z² = 1 - x² - y², soit [x(w - x)/(y² - x(w-x))]² = ((w-x)² - w² + x² + y²)/(w² - x² - y²)
En normalisant à w = 1 on obtient la sextique :

x²(1 - x)²(1 - x² - y²) = (2x² + y² - 2x)(x² + y² - x)² [1]

Que l'on peut exprimer sous forme d'une équation du troisième degré en Y = y² :

Y³ - 4x(1 - x)Y² - 6x²(1 - x)²Y - x²(1 - x)³(3x + 1) = 0

Pour 0 < x < 1, cette équation a une seule solution réelle et on peut ainsi appliquer les formules de Cardan avec seulement des nombres réels.
Pour simplifier l'applet, cette frontière n'est pas prise en compte dans la limitation physique de X et Y, contrairement aux autres contraintes. (les formules de Cardan étant ... assez compliquées ...)
Pour simplifier l'applet, la frontière est d'ailleurs ici une approximation (en orange).

Prendre le morceau commun dans le carré y² est encore pire (découpe P-strip en gris).

Conclusion sur cette dissection

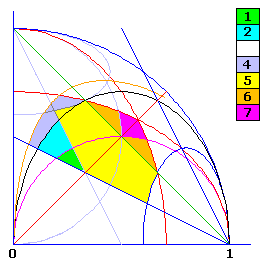
En conclusion, avec la seule contrainte y<z (soit "par convention"), les domaines de validité de cette dissection sont :

x<y<z : y<x<z : y<z<x : En dehors de ces régions (parties non coloriées), cette dissection est impossible.

Il reste à normaliser les deux cas y<x<z et y<z<x en x<y<z par changement de variables, pour avoir unicité des points (x,y).

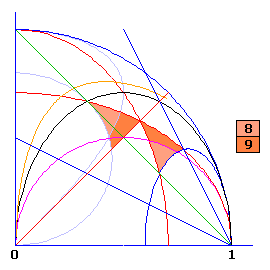
Le premier cas s'obtient juste en échangeant x et y (symétrie par rapport à la droite à 45°) et les régions 5', 6' et 7'.
Le second est un peu plus compliqué car il faut effectuer une permutation circulaire, (x, y, z) → (y, z, x) et la transformation sur z est quadratique, soit : (x, y) → (y,  √1 - x² - y² )
Les régions 8' et 9' sont ainsi déformées par rapport aux régions 8 et 9.
Les régions (8' + 9') recouvrent les régions (5' + 6' + 7')    [a]
On notera des reliquats des régions 1, 2 et 4 pour lesquelles la seule dissection est avec x inchangé.
En grisé les frontières transformées par changement de variable.
Le cas [a] pour lequel on peut choisir n'importe lequel des trois carrés inchangé est défini par

25y² >  4(2 - 5x²) + 8√4 - 5x²

(transformée de (5x - 4)² + 5y² - 1 > 0, possibilité du P-slide de z, dans le domaine "normalisé" x<y<z)
Les sommets de ce domaine étant les points [x = 4/9, y = 4/9], [ x =  1/√3 , y = 1/√3 ] et [x = 1/3, y = 2/3]
En particulier la région 3 (recouvrement, y² horizontal, z² vertical) est dans ce domaine. Plus un petit bout des régions 1 et 2.

Nous ne chercherons pas à regrouper tout ceci en un seul diagramme !
On remarque toutefois que le choix de y ou z comme carré intact n'apporte rien de plus :

S'il est possible d'effectuer la dissection avec y ou z inchangé, il est alors possible de l'effectuer avec x inchangé. S'il est possible d'effectuer la dissection avec z inchangé, il est aussi possible de l'effectuer avec x ou y inchangé [a].

Par contre il y a effectivement des régions où seul le choix de x est possible (parties de 1, 2 et 4).
Noter que remplacer des P-slide par des P-strip quand c'est possible fournit des variantes de cette disection.

En dehors du domaine de validité de cette dissection, il est nécessaire d'utiliser la dissection suivante :

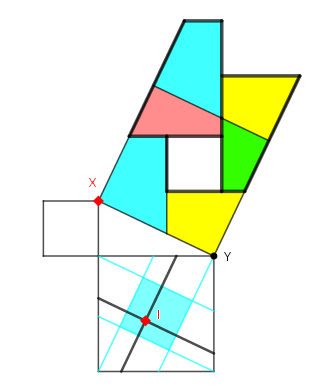
Perigal

La dissection de Perigal est celle de 2 carrés en un seul choisie comme emblème de ce sujet sur les dissections. Elle peut être considérée comme une superposition de pavages. L'un avec le grand carré, l'autre formé des deux petits.
Cette superposition peut être excentrée pour donner des variantes de cette dissection.
Dans l'applet ci-contre, (Geogebra, cliquer) le point X est déplaçable pour définir x/y < 1.
Le point I initialement centré est déplaçable dans la zone bleue.

Appliquons cette dissection au carré w² ↔ z² + (x² + y²), et choisissons l'excentricité maximale conservant le "petit" carré (x² + y²) non encore découpé et donnant la plus grande pièce possible dans le carré z² : cette découpe passe par les sommets du carré z², I est à un sommet de sa zone autorisée.
Reste à choisir judicieusement le découpage pour (x² + y²) ↔ x² + y², car sinon on obtient une dissection en 9 morceaux. (les 4 de z², les 4 de y² et le carré x² inchangé)
L'astuce géniale de Frederickson est de regrouper et redécouper diverses pièces de cette dissection en 9 morceaux pour économiser une pièce et obtenir une dissection en 8 morceaux seulement.

Le carré y² est ainsi découpé en deux pièces seulement, pour donner une forme "exotique" en 3 morceaux, d'aire x² + y² et de largeur  √x² + y². (en gras dans l'applet) : Deux des pièces du découpage de Perigal sont déplacées en dehors du carré et recollées aux autres
Le bord du "parallèloïde" (polygone formé par translation d'un zig-zag) ainsi construit définit la découpe supplémentaire dans la plus grande pièce du carré z²

Et finallement la construction complète suivante.
Dans cette applet les points X,Y définissent x,y et ces valeurs sont reportées dans le diagramme xy.
Les décalages des découpes de Perigal sont réglables par les points bleus.
'O', '0' et '1' définissent les cadrages et le zoom.

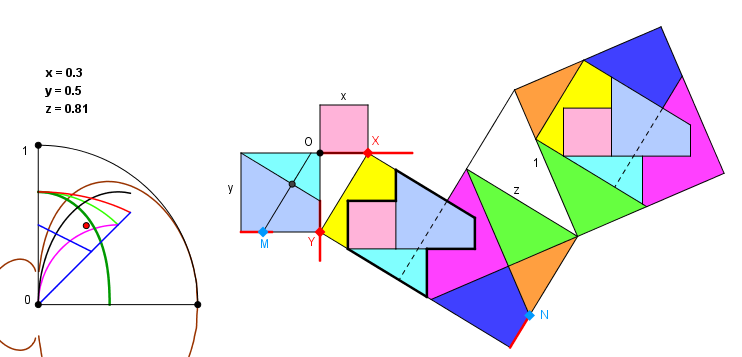
Il est possible de retourner la découpe du carré y² par rapport à celle du carré z², en construisant les carrés z² et w² dans l'autre sens par rapport à la médiatrice de XY, mais cette variante est moins générale : à l'intérieur du demi-cercle magenta (2x - 1)² + 4y² = 1 la frontière est plus restrictive.

Bien entendu tout ceci n'a de sens que si le plus grand carré de z² et (x² + y²) est z², et évidemment x < y !
Soit z² > x² + y² ou encore z > w/√2, soit à l'intérieur du 1/8 de cercle 2x² + 2y² = 1 en vert clair dans le diagramme.
En fait la limitation principale vient de la découpe en zig-zag de la grande pièce du carré z², qui ne doit pas déborder.

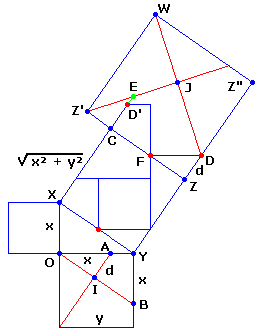
Dans la découpe du carré y² on obtient le débordement : d/x = x/√x² + y² (triangles OAI et OBY semblables), soit d = x²/√x² + y²
Dans la découpe du carré z² la limite est alors ZD = d < z - √x² + y² d'où  x²/√x² + y² < z - √x² + y² et après simplification la condition :

z > (2x² + y²)/√x² + y² [2]

Dans le plan (x,y) ceci donne, en substituant z² = 1 - x² - y² :
(1 - x² - y²)(x² + y²) - (2x² + y²)² < 0

Cette condition, matérialisée par la quartique correspondante en vert foncé dans le diagramme, est plus restrictive car cette quartique est intérieure au quart de cercle 2x² + 2y² = 1.

Il reste à vérifier l'autre coin D' avec la limite précédente.
Les triangles semblables dans le carré z² donnent CE/CZ' = Z"W/Z"D
Comme on est sur la limite précédente, CZ' = d et CE = d × z/(z - d) > d
Cette condition est donc toujours satisfaite si la condition précédente l'est, et la pièce magenta ne dégénère jamais.

Dans l'applet x,y sont déplaçables dans tout le domaine de définition x < y < z, mais au delà de la quartique, la construction échoue (des pièces débordent ou se chevauchent). A la limite, sur la quartique, il est inévitable de séparer la pièce jaune en deux pièces reliées par un seul point. La découpe ne marche ainsi en pratique que suffisamment "loin" de cette limite.

Conclusion

Les trois classes indiquées par Frederickson sont ainsi

1. - (x, y) au dessous de la quartique [2] : dissection à la Perigal
2. - sinon au dessus du demi-cercle (2x - 1)² + 4y² = 1 : rectangles avec recouvrement
3. - au dessous du demi-cercle : rectangles avec débordement

Ces deux dernières classes peuvent parfois être aussi réalisables "à la Perigal".
Ceci nécessite que le rectangle d'aire y² ne soit pas trop aplati, soit x + 2y < w
Si ce rectangle est trop aplati et donc la dissection en rectangles ne marche pas, alors la condition [2] est satisfaite et la dissection à la Perigal marche toujours.
En effet w > x + 2y ⇔ z² > 3y² + 4xy et 3y² + 4xy > (2x² + y²)²/(x² + y²) pour y > x. Le calcul est élémentaire et laissé au lecteur.

Il existe malheureusement dans le cas 2 un cas d'impossibilité non traité :
Au dessus de la quartique [2] et au dessus de la sextique [1] (et bien entendu au dessous de l'ellipse matérialisant x≤y≤z)
Par exemple x = 1, y = 4, z = √19, w = 6 (0.166, 0.666, 0.726, 1 en coordonnées réduites)

Les sommets de la zone impossible, sur la sextique [1], sont :
[x = 0.2137403627835, y = 0.6907659269864] (sur l'ellipse y<z)
[x = 0.17941527446301, y = 0.6591739252599] (sur la quartique [2])

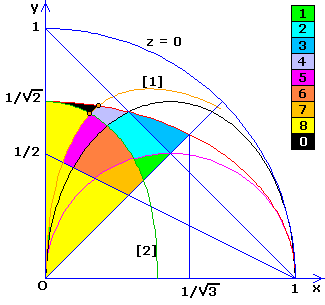En résumé dans le diagramme suivant :

Rectangles seulement :

Au choix, Perigal ou rectangles

 8  : Perigal seulement

 0  : Aucune dissection connue en 8 pièces seulement
Bien entendu, une dissection en 9 pièces est possible dans ce cas...

En omettant les détails des régions pour lesquelles la découpe en rectangles peut se faire aussi avec y ou z intact, au lieu du plus petit x.